题目内容
 如图,已知直角三角形ABC的周长为
如图,已知直角三角形ABC的周长为 ,斜边上的中线CD=1,则△ABC的面积为
,斜边上的中线CD=1,则△ABC的面积为
- A.

- B.

- C.

- D.1
B
分析:根据直角三角形斜边上的中线等于斜边的一半求出AB,然后根据三角形的周长求出AC+BC,再平方并利用勾股定理求出AC•BC,然后根据三角形的面积公式列式进行计算即可得解.
解答:∵斜边上的中线CD=1,
∴AB=2CD=2×1=2,
∵△ABC的周长为2+ ,
,
∴AC+BC=2+ -2=
-2= ,
,
∴(AC+BC)2=AC2+2AC•BC+BC2=5,
根据勾股定理,AC2+BC2=AB2=4,
∴AC•BC= ,
,
∴△ABC的面积= AC•BC=
AC•BC= ×
× =
= .
.
故选B.
点评:本题主要考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的应用,利用完全平方公式以及勾股定理求出AC•BC= 是解题的关键.
是解题的关键.
分析:根据直角三角形斜边上的中线等于斜边的一半求出AB,然后根据三角形的周长求出AC+BC,再平方并利用勾股定理求出AC•BC,然后根据三角形的面积公式列式进行计算即可得解.
解答:∵斜边上的中线CD=1,
∴AB=2CD=2×1=2,
∵△ABC的周长为2+
 ,
,∴AC+BC=2+
 -2=
-2= ,
,∴(AC+BC)2=AC2+2AC•BC+BC2=5,
根据勾股定理,AC2+BC2=AB2=4,
∴AC•BC=
 ,
,∴△ABC的面积=
 AC•BC=
AC•BC= ×
× =
= .
.故选B.
点评:本题主要考查了直角三角形斜边上的中线等于斜边的一半的性质,勾股定理的应用,利用完全平方公式以及勾股定理求出AC•BC=
 是解题的关键.
是解题的关键. 
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
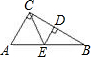 如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )| A、AE=BE | ||
B、CE=
| ||
| C、∠CEB=2∠A | ||
D、AC=
|
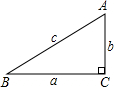 如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )
如图,已知直角三角形ABC的三边分别为a、b、c,则sinA等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 (2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y=
(2012•上城区二模)如图,已知直角三角形OAB的直角边OA在x轴上,双曲线y= 如图,已知直角三角形ABC的周长为
如图,已知直角三角形ABC的周长为