题目内容
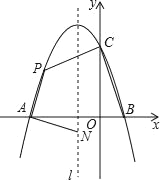
【题目】如图,![]() 是自动喷灌设备的水管,点
是自动喷灌设备的水管,点![]() 在地面,点
在地面,点![]() 高出地面
高出地面![]() 米.在
米.在![]() 处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头
处有一自动旋转的喷水头,在每一瞬间,喷出的水流呈抛物线状,喷头![]() 与水流最高点
与水流最高点![]() 的连线与水平线成
的连线与水平线成![]() 角,水流的最高点
角,水流的最高点![]() 与喷头
与喷头![]() 高出
高出![]() 米,在如图的坐标系中,水流的落地点
米,在如图的坐标系中,水流的落地点![]() 到点
到点![]() 的距离是________米.
的距离是________米.

【答案】![]()
【解析】
根据所建坐标系,易知B点坐标和顶点C的坐标,设抛物线解析式为顶点式,可求表达式,求AD长就是求y=0是x的值.
如图,建立直角坐标系,过C点作CE⊥y轴于E,过C点作CF⊥x轴于F,
∴B(0,1.5),
∴∠CBE=45°,
∴EC=EB=2米,
∵CF=AB+BE=2+1.5=3.5,
∴C(2,3.5)
设抛物线解析式为:y=a(x-2)2+3.5,
又∵抛物线过点B,
∴1.5=a(0-2)2+3.5
∴a=-![]() ,
,
∴y=-![]() (x-2)2+3.5=-
(x-2)2+3.5=-![]() x2+2x+
x2+2x+![]() ,
,
∴所求抛物线解析式为:y=-![]() x2+2x+
x2+2x+![]() ,
,
∵抛物线与x轴相交时,y=0,
∴![]() ,
,
∴x1=![]() ,x2=
,x2=![]() (舍去)
(舍去)
∴D(![]() ,0)
,0)
∴水流落点D到A点的距离为:![]() 米.
米.

故答案为:![]()

练习册系列答案
相关题目