题目内容
如果若多项式x2-(k+1)x+49是一个完全平方式,则k= .
考点:完全平方式
专题:
分析:根据完全平方式的形式是a2±2ab+b2,先确定出a、b对应的值,即可求出k的值.
解答:解:∵多项式x2-(k+1)x+49是一个完全平方式,
∴x2-(k+1)x+49=(x±7)2=x2±14x+49,
∴k+1=±14,
解得:k=-15或13.
故答案为:-15或13.
∴x2-(k+1)x+49=(x±7)2=x2±14x+49,
∴k+1=±14,
解得:k=-15或13.
故答案为:-15或13.
点评:本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
下列计算中正确的是( )
| A、y6÷y6=1 |
| B、(3ab2)2=6a2b4 |
| C、a3•a2=a6 |
| D、y6+y6=2y12 |
 如图,等边△ABC的边长为7cm,M为△ABC内任意一点,MD∥AC,ME∥AB,MF∥BC,求MD+ME+MF的值.
如图,等边△ABC的边长为7cm,M为△ABC内任意一点,MD∥AC,ME∥AB,MF∥BC,求MD+ME+MF的值. 如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
如图,将二次函数y=x2-m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法: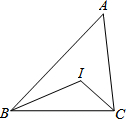 如图,△ABC中,点I是∠ABC、∠ACB角平分线的交点,∠BIC=130°,则∠A=
如图,△ABC中,点I是∠ABC、∠ACB角平分线的交点,∠BIC=130°,则∠A=