题目内容
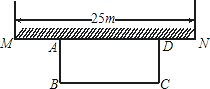
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
题目内容
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案