题目内容
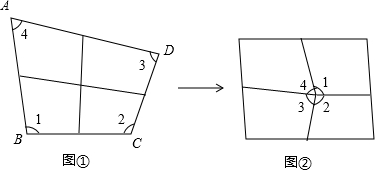
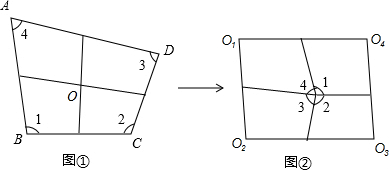
如图,将四边形纸片ABCD沿着BD折叠,A点恰好落在BC上(BC>AB).再将四边形纸片ABCD的B点折向D,此时CB与CD恰好重合,得到折线CE.E点落在AD上,则下列结论正确的是
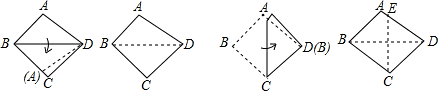
- A.AB∥CD
- B.AD∥BC
- C.∠ADB=∠BDC
- D.∠ADB>∠BDC
A
分析:由A点落在BC上,折线为BD,根据折叠的性质得到∠ABD=∠CBD,又B点折向D,使得B、D两点重合,折线为CE,再根据折叠的性质得到CD=CB,然后转化为角相等,这样就有∠ABD=∠CDB,根据平行线的判定定理即可得到A正确.
解答:∵A点落在BC上,折线为BD,
∴∠ABD=∠CBD,
又∵B点折向D,使得B、D两点重合,折线为CE,
∴CD=CB,
∴∠CBD=∠CDB,
∴∠ABD=∠CDB,
∴AB∥CD.
故A正确;
若AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵BC=CD,
∴四边形ABCD是菱形,
∴AB=BC与BC>AB矛盾,
∴AD与BC不平行;
故B错误;
∵如图,将四边形纸片ABCD沿着BD折叠,A点恰好落在BC上(BC>AB),
∴∠ADB<∠BDC,
故C、D错误.
故选:A.
点评:此题考查了折叠的性质、等腰三角形的性质以及平行线的判定.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.
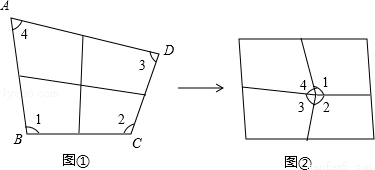
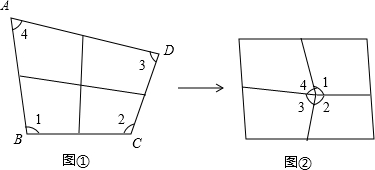
分析:由A点落在BC上,折线为BD,根据折叠的性质得到∠ABD=∠CBD,又B点折向D,使得B、D两点重合,折线为CE,再根据折叠的性质得到CD=CB,然后转化为角相等,这样就有∠ABD=∠CDB,根据平行线的判定定理即可得到A正确.
解答:∵A点落在BC上,折线为BD,
∴∠ABD=∠CBD,
又∵B点折向D,使得B、D两点重合,折线为CE,
∴CD=CB,
∴∠CBD=∠CDB,
∴∠ABD=∠CDB,
∴AB∥CD.
故A正确;
若AD∥BC,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵BC=CD,
∴四边形ABCD是菱形,
∴AB=BC与BC>AB矛盾,
∴AD与BC不平行;
故B错误;
∵如图,将四边形纸片ABCD沿着BD折叠,A点恰好落在BC上(BC>AB),
∴∠ADB<∠BDC,
故C、D错误.
故选:A.
点评:此题考查了折叠的性质、等腰三角形的性质以及平行线的判定.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目