题目内容
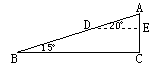
 如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D点,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点,用了10分钟.求山高(即AC的长度)及A、B两点的水平距离(即BC的长度)(精确到0.01千米).(sin15°=0.2588,cos15°=0.9659,sin20°=0.3420,cos20°=0.9397)
如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D点,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点,用了10分钟.求山高(即AC的长度)及A、B两点的水平距离(即BC的长度)(精确到0.01千米).(sin15°=0.2588,cos15°=0.9659,sin20°=0.3420,cos20°=0.9397)
分析:过D作DF⊥BC于F,分别利用坡角及三角函数求出BF,DE,AE,DF的值即可求得AC,BC的长.
解答: 解:过D作DF⊥BC于F.
解:过D作DF⊥BC于F.
∴BC=BF+FC=BF+DE=BD•cos15°+AD•cos20°=5×
×0.9659+3×
×0.9397≈1.44(千米).
AC=AE+EC=AE+DF=AD•sin20°+BD•sin15°=3×
×0.3420+5×
×0.2588≈0.43(千米).
答:山高为0.43千米,A、B两点的水平距离为1.44千米.
 解:过D作DF⊥BC于F.
解:过D作DF⊥BC于F.∴BC=BF+FC=BF+DE=BD•cos15°+AD•cos20°=5×
| 12 |
| 60 |
| 10 |
| 60 |
AC=AE+EC=AE+DF=AD•sin20°+BD•sin15°=3×
| 10 |
| 60 |
| 12 |
| 60 |
答:山高为0.43千米,A、B两点的水平距离为1.44千米.
点评:此题主要考查学生对坡度坡角的理解及三角函数的综合运用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,一勘测人员从山脚B点出发,沿坡度为1:3的坡面BD行至D点处时,他的垂直高度上升了15米;然后再从D点处沿坡角为45°的坡面DA以20米/分钟的速度到达山顶A点时,用了10分钟.
如图,一勘测人员从山脚B点出发,沿坡度为1:3的坡面BD行至D点处时,他的垂直高度上升了15米;然后再从D点处沿坡角为45°的坡面DA以20米/分钟的速度到达山顶A点时,用了10分钟. 如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处,用了10分钟,求山高(即AC的长度)及(即BC的长)(精确到0.01千米).
如图,一勘测人员从B点出发,沿坡角为15°的坡面以5千米/时的速度行至D处,用了12分钟,然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处,用了10分钟,求山高(即AC的长度)及(即BC的长)(精确到0.01千米).