题目内容

计算：
（1）（
1
4
）-2×（2-4×80）；
（2）3x•（x3）3÷x2-2x2•3x3．
考点：整式的混合运算,零指数幂,负整数指数幂
专题：
分析：（1）先根据负整数指数幂定义变形，再根据同底数幂的乘法法则进行计算，即可求出答案；
（2）先算乘方，再算乘除即可．
解答：解：（1）原式=42×2-4×1
=24×2-4
=20
=1；

（2）原式=3x•x9÷x2-6x5
=3x8-6x5．
点评：本题考查了整式的混合运算，负整数指数幂定义，同底数幂的乘法法则，零指数幂的应用，主要考查学生的计算能力．
练习册系列答案
相关题目
若A（x1，y1），B（x2，y2），C（x3，y3）是反比例函数y=
k2+1
x
图象上的点，且x1＜x2＜0＜x3，则y1、y2、y3的大小关系正确的是（　　）
A、y3＞y1＞y2
B、y1＞y2＞y3
C、y2＞y1＞y3
D、y3＞y2＞y1
如图，为了绿化小区，某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH．已知：PH∥AE，PK∥BC，DE=100米，EA=60米，BC=70米，CD=80米．以BC所在直线为x轴，AE所在直线为y轴，建立平面直角坐标系，坐标原点为O．
（Ⅰ）求直线AB的解析式．
（Ⅱ）若设点P的横坐标为x，矩形PKDH的面积为S．
（1）用x表示S；
（2）当x为何值时，S取最大值，并求出这个最大值．
求不等式组
3x+2＞2(x-1)
x+8＞4x-1
的解集．
第20届世界杯足球赛正在如火如荼的进行，爸爸想通过一个游戏决定小明能否看今晚的比赛：在一个不透明的盒子中放入三张卡片，每张卡片上写着一个实数，分别为3，
2
，2
2
（每张卡片除了上面的实数不同以外其余均相同），爸爸让小明从中任意取一张卡片，如果抽到的卡片上的数是有理数，就让小明看比赛，否则就不能看．
（1）请你直接写出按照爸爸的规则小明能看比赛的概率；
（2）小明想了想，和爸爸重新约定游戏规则：自己从盒子中随机抽取两次，每次抽取一张卡片，第一次抽取后记下卡片上的数，再将卡片放回盒中抽取第二次，如果抽取的两数之积是有理数，自己就看比赛，否则就不看．请你用列表法或树状图法求出按照此规则小明看比赛的概率．
受国内外复杂多变的经济环境影响，去年1至7月，原材料价格一路攀升，义乌市某服装厂每件衣服原材料的成本y1（元）与月份x（1≤x≤7，且x为整数）之间的函数关系如下表：
月份x1234567
成本（元/件）56586062646668
8至12月，随着经济环境的好转，原材料价格的涨势趋缓，每件原材料成本y2（元）与月份x的函数关系式为y2=x+62（8≤x≤12，且x为整数）．
（1）请观察表格中的数据，用学过的函数相关知识求y1与x的函数关系式．
（2）若去年该衣服每件的出厂价为100元，生产每件衣服的其他成本为8元，该衣服在1至7月的销售量p1（万件）与月份x满足关系式p1=0.1x+1.1（1≤x≤7，且x为整数）； 8至12月的销售量p2（万件）与月份x满足关系式p2=-0.1x+3（8≤x≤12，且x为整数），该厂去年哪个月利润最大？并求出最大利润．
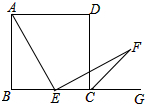如图，在正方形ABCD中，边长AB=3，点E（与B，C不重合）是BC边上任意一点，把EA绕点E顺时针方向旋转90°到EF，连接CF．
（1）求证：CF是正方形ABCD的外角平分线；
（2）当∠BAE=30°时，求CF的长．
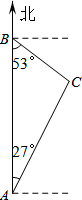如图，禁渔期间，我渔政船在A处发现正北方向B处有一艘可疑船只，测得A、B两处距离为99海里，可疑船只正沿南偏东53°方向航行．我渔政船迅速沿北偏东27°方向前去拦截，2小时后刚好在C处将可疑船只拦截．求该可疑船只航行的速度．
（参考数据：sin27°≈
9
20
，cos27°≈
9
10
，tan27°≈
1
2
，sin53°≈
4
5
，cos53°≈
3
5
，tan53°≈
4
3
）
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米．某天该深潜器在海面下1800米的A点处作业（如图），测得正前方海底沉船C的俯角为45°，该深潜器在同一深度向正前方直线航行2000米到B点，此时测得海底沉船C的俯角为60°．
（1）沉船C是否在“蛟龙”号深潜极限范围内？并说明理由；
（2）由于海流原因，“蛟龙”号需在B点处马上上浮，若平均垂直上浮速度为2000米/时，求“蛟龙”号上浮回到海面的时间．（参考数据：
2
≈1.414，
3
≈1.732）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网