题目内容
 如图,要在河的一侧测量对岸水塔的高度,小明设计了如下的测量方案:先在河的这侧选取一点A,测得水塔顶点O的仰角为30°,再朝着水塔方向前进20米到达B处,这时测得与水塔顶点O的仰角为45°,你能根据这些数据算出水塔高度吗?(结果可保留根号)
如图,要在河的一侧测量对岸水塔的高度,小明设计了如下的测量方案:先在河的这侧选取一点A,测得水塔顶点O的仰角为30°,再朝着水塔方向前进20米到达B处,这时测得与水塔顶点O的仰角为45°,你能根据这些数据算出水塔高度吗?(结果可保留根号)
分析:首先分析图形:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答: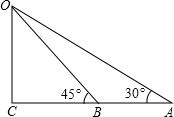 解:设水塔高度为x米,在Rt△OBC中,
解:设水塔高度为x米,在Rt△OBC中,
∵∠OBC=45°,
∴BC=OC=x,
在Rt△OAC中
=tan30°,
∴
=
,
即3x-
x=20
,
解得x=
=10+10
,
答:水塔高度为(10+10
)米.
 解:设水塔高度为x米,在Rt△OBC中,
解:设水塔高度为x米,在Rt△OBC中,∵∠OBC=45°,
∴BC=OC=x,
在Rt△OAC中
| OC |
| AC |
∴
| x |
| x+20 |
| ||
| 3 |
即3x-
| 3 |
| 3 |
解得x=
20
| ||
3-
|
| 3 |
答:水塔高度为(10+10
| 3 |
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目

 如图,要在河的一侧测量对岸水塔的高度,小明设计了如下的测量方案:先在河的这侧选取一点A,测得水塔顶点O的仰角为30°,再朝着水塔方向前进20米到达B处,这时测得与水塔顶点O的仰角为45°,你能根据这些数据算出水塔高度吗?(结果可保留根号)
如图,要在河的一侧测量对岸水塔的高度,小明设计了如下的测量方案:先在河的这侧选取一点A,测得水塔顶点O的仰角为30°,再朝着水塔方向前进20米到达B处,这时测得与水塔顶点O的仰角为45°,你能根据这些数据算出水塔高度吗?(结果可保留根号)