题目内容
如图,在平面直角坐标系中,直线 :
: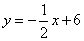 分别与
分别与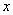 轴、
轴、 轴交于点B、C,且与直线
轴交于点B、C,且与直线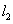 :
: 交于点A.
交于点A.
(1)分别求出点A、B、C的坐标;
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的函数表达式;
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
 |
解:(1)直线 :
: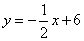 ,
,
当 时,
时, ,
,
当 时,
时, ,
,
∴B(12,0),C(0,6),
解方程组: 得:
得:
∴A(6,3),
答:A(6,3),B(12,0),C(0,6).
(2)解:设D ,
,
∵△COD的面积为12,
∴ ,
,
解得: ,
,
∴D(4,2),设直线CD的函数表达式是 ,
,
把C(0,6),D(4,2)代入得:

解得:
∴ ,
,
答:直线CD的函数表达式是 .
.
(3)答:存在点Q,使以O、C、P、Q为顶点的四边形是菱形,点Q的坐标是
(6,6)或(-3,3)或


 导学全程练创优训练系列答案
导学全程练创优训练系列答案如图是由5个大小相同的正方体组成的几何体,它的主视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
(1)阅读合作学习内容,请解答其中的问题;
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
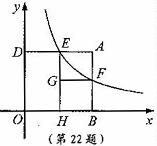 针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由。
针对小亮提出的问题,请你判断这两个矩形能否全等?直接写出结论即可;这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由。
下列各组条件中,不能判定△ABC≌△A′B′C′的是( )
|
| A. | AC=A′C′,BC=B′C′,∠C=∠C′ | B. | ∠A=∠A′,BC=B′C′,AC=A′C′ |
|
| C. | AC=A′C′,AB=A′B′,∠A=∠A′ | D. | AC=A′C′,∠A=∠A′,∠C=∠C′ |




 的图象分别相交于点E,F,且DE=2,过点E作EH⊥
的图象分别相交于点E,F,且DE=2,过点E作EH⊥ 轴于点H,过点F作FG⊥EH于点G。回答下列问题:
轴于点H,过点F作FG⊥EH于点G。回答下列问题: 有两相异实根,则
有两相异实根,则 的取值范围是 .
的取值范围是 .  .
. 取任何实数,方程总有两个不相等的实数根;
取任何实数,方程总有两个不相等的实数根; .
.