题目内容
如图，在等边三角形ABC中，AE=CD，AD、BE相交于P点．∠BPD=________°．
60
分析：易证△ABD≌△CBE，得∠BAD=∠CBE，根据∠ABD+∠BAD+∠ADB=180°，∠EBD+∠ADB+∠BPD=180°，可证∠BPD=∠ABD，即可解题．
解答：∵AE=CD，∴CE=BD，
∵∠ABD=∠BCE，AB=BC，
∴△ABD≌△CBE，故∠BAD=∠CBE，
∵∠ABD+∠BAD+∠ADB=180°，
∠CBE+∠ADB+∠BPD=180°，
∴∠BPD=∠ABD，
∵∠ABD=60°，∴∠BPD=60°，
故答案为 60°．
点评：本题考查了等边三角形内角为60°的性质，考查了三角形内角和为180°的性质，考查了全等三角形的证明和对应角相等的性质，本题中求证△ABD≌△CBE是解题的关键．
分析：易证△ABD≌△CBE，得∠BAD=∠CBE，根据∠ABD+∠BAD+∠ADB=180°，∠EBD+∠ADB+∠BPD=180°，可证∠BPD=∠ABD，即可解题．
解答：∵AE=CD，∴CE=BD，
∵∠ABD=∠BCE，AB=BC，
∴△ABD≌△CBE，故∠BAD=∠CBE，
∵∠ABD+∠BAD+∠ADB=180°，
∠CBE+∠ADB+∠BPD=180°，
∴∠BPD=∠ABD，
∵∠ABD=60°，∴∠BPD=60°，
故答案为 60°．
点评：本题考查了等边三角形内角为60°的性质，考查了三角形内角和为180°的性质，考查了全等三角形的证明和对应角相等的性质，本题中求证△ABD≌△CBE是解题的关键．
练习册系列答案
相关题目
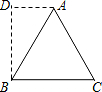如图，在等边三角形ABC的边BC、AC上分别取点D、E，使BD=CE，AD与BE相交于点P．则∠APE的度数为
9、如图，在等边三角形ABC中，三条中线AE，BD，CF相交于点O，则等边三角形ABC中，从△BOF到△COD需要经过的变换是（ ）
如图，在等边三角形ABC中，BD⊥BC，过A作AD⊥BD于D，已知△ABC周长为M，则AD=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使CE=CD，求证：△BDE为等腰三角形．
如图，在等边三角形△ABC中，AQ=PQ，PR⊥AB于点R，PS⊥AC于点S，且PR=PS，下面给出的四个结论：①点P在∠A的平分线上，②AS=AR，③QP∥AR，④△BRP≌△QSP，则其中正确的是（ ）