题目内容
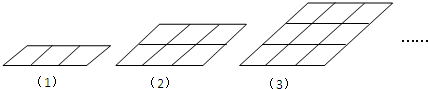
如图所示第(1)个图形中有6个平行四边形,第(2)个图形中有18个平行四边形,根据上述规律,则第(3)个图形中有 个平行四边形,依次下去第n个图形中有 个平行四边形.(用含n的代数式表示)

考点:规律型:图形的变化类
专题:
分析:由于图①平行四边形有6个=6×1,图②平行四边形有18个=6×(2+1),图③平行四边形有36个=6×(1+2+3),由此即可得到第⑥个图形中平行四边形的个数.
解答:解:∵第①个图形中一共有6个平行四边形,第②个图形中一共有18个平行四边形,第③个图形中一共有36个平行四边形,…,
∵图①平行四边形有6个=6×1,
图②平行四边形有18个=6×(1+2),
图③平行四边形有36个=6×(1+2+3),
∴第n个图形中平行四边形的个数为:6×(1+2+3+4+5+6+…+n)=3n(n+1).
故答案为:36,3n(n+1).
∵图①平行四边形有6个=6×1,
图②平行四边形有18个=6×(1+2),
图③平行四边形有36个=6×(1+2+3),
∴第n个图形中平行四边形的个数为:6×(1+2+3+4+5+6+…+n)=3n(n+1).
故答案为:36,3n(n+1).
点评:此题主要考查了图形的变化规律,是根据图形进行数字猜想的问题,关键是通过归纳与总结,得到其中的规律,然后利用规律解决一般问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一等腰三角形的两边长分别为8cm、4cm,那么该等腰三角形的周长为( )
| A、20cm |
| B、16cm |
| C、20cm或16cm |
| D、以上都不正确 |
如果把分式
中的x、y同时扩大为原来的3倍,则分式的值( )
| x2 |
| x+y |
| A、保持不变 |
| B、是原来的3倍 |
| C、是原来的9倍 |
| D、无法确定 |

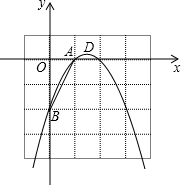 如图,已知抛物线y1=-x2+bx+c经过A(1,0),B(0,-2)两点,顶点为D.
如图,已知抛物线y1=-x2+bx+c经过A(1,0),B(0,-2)两点,顶点为D. 如图:等腰三角形△ABC中,AB=AC,BD平分∠ABC,如果AD=BD=BC,则∠A=
如图:等腰三角形△ABC中,AB=AC,BD平分∠ABC,如果AD=BD=BC,则∠A=