题目内容
某班四个小组进行辩论比赛,赛前三位同学预测比赛结果如下:
甲说:“第二组得第一,第四组得第三”;
乙说:“第一组得第四,第三组得第二”;
丙说:“第三组得第三,第四组得第一”;
赛后得知,三人各猜对一半,则冠军是( )
甲说:“第二组得第一,第四组得第三”;
乙说:“第一组得第四,第三组得第二”;
丙说:“第三组得第三,第四组得第一”;
赛后得知,三人各猜对一半,则冠军是( )
| A、第一组 | B、第二组 |
| C、第三组 | D、第四组 |
考点:推理与论证
专题:
分析:分别假设甲、乙、丙三人所说的其中一句话正确,进而分析得出符合题意的答案.
解答:解:假设甲说的第一句对,第二组得第一对,则第四组得第三错;
由此可知,丙说的第四组得第一错,则第三组得第三对;
则乙说的:第一组得第四对,第三组得第二错,
由此可推知:第二组第一,第四组第二,第三组第三,第一组第4,符合题意;
假设甲说的第一句错,第二组得第一错,则第四组得第三对;
由此可知,丙说的第四组得第一错,则第三组得第三错;与已知出现矛盾,故此推理错误;
故选:B.
由此可知,丙说的第四组得第一错,则第三组得第三对;
则乙说的:第一组得第四对,第三组得第二错,
由此可推知:第二组第一,第四组第二,第三组第三,第一组第4,符合题意;
假设甲说的第一句错,第二组得第一错,则第四组得第三对;
由此可知,丙说的第四组得第一错,则第三组得第三错;与已知出现矛盾,故此推理错误;
故选:B.
点评:此题主要考查了推理与论证,通过假设其中一句话是正确的,根据所给条件进行推理,与题意相符则正确,与题意矛盾则排除是完成此类问题的基本思路.

练习册系列答案
相关题目
若顺次连接四边形ABCD各边的中点所得四边形是菱形.则四边形ABCD一定是( )
| A、菱形 |
| B、对角线互相垂直的四边形 |
| C、平行四边形 |
| D、对角线相等的四边形 |
衢州上下街因衢江流向而得名,至今已有六七百年的历史,有“衢州第一街”的美誉,今年市政府决定再投资2630万元用于道路改造,把上下街建成一个高起点、高标准、高品质的娱乐、休闲、赏景为一体的商业街.将2630万元用科学记数法表示为( )元.
| A、26.3×106 |
| B、2.63×107 |
| C、2.63×106 |
| D、26.3×107 |
等腰三角形的对称轴最多有( )条.
| A、1 | B、2 | C、3 | D、4 |
函数y=
中自变量x的取值范围是( )
| x | ||
|
| A、x>-1 |
| B、x≥-1 |
| C、x>-1且x≠0 |
| D、x≥-1且x≠0 |
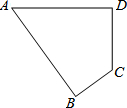 如图,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.
如图,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.