题目内容
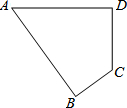 如图,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.
如图,在多边形ABCD中,AB=2,CD=1,∠A=45°,∠B=∠D=90°,求多边形ABCD的面积.考点:等腰直角三角形
专题:
分析:如图,延长BC和AD交于点E,则△ABE和△CDE都是等腰直角三角形,所以四边形ABCD的面积=两三角形面积之差.
解答: 解:如图,延长BC和AD交于点E.
解:如图,延长BC和AD交于点E.
∵∠A=45°,∠B=∠D=90°,
∴易得△ABE和△CDE都是等腰直角三角形,
∴AB=BE,CD=DE,
∴S四边形ABCD=S△ABE-S△CDE=
AB•AB-
CD•CD=
×2×2-
×1×1=
.即:多边形ABCD的面积是
.
 解:如图,延长BC和AD交于点E.
解:如图,延长BC和AD交于点E.∵∠A=45°,∠B=∠D=90°,
∴易得△ABE和△CDE都是等腰直角三角形,
∴AB=BE,CD=DE,
∴S四边形ABCD=S△ABE-S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查了等腰直角三角形.根据题意作出辅助线是解题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目