题目内容
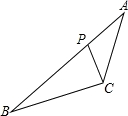
如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证: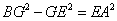 .
.

(1)BH=AC,理由如下:
 ∵CD⊥AB,BE⊥AC,
∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°,
∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD,
∵在△DBH和△DCA中
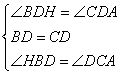 ,∴△DBH≌△DCA(ASA),∴BH=AC.
,∴△DBH≌△DCA(ASA),∴BH=AC.
(2)连接CG,
由(1)知,DB=CD,∵F为BC的中点,
∴DF垂直平分BC,∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC,∴EC=EA,
在Rt△CGE中,由勾股定理得: ,
,
∵CE=AE,BG=CG,∴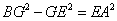 .
.

练习册系列答案
相关题目
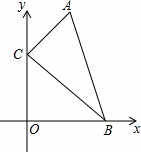
 =
= 中的自变,量
中的自变,量 的取值范围是 .
的取值范围是 .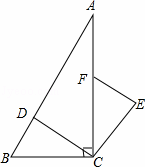 (1)求证:△BCD≌△FCE;
(1)求证:△BCD≌△FCE; 在第二象限,则点
在第二象限,则点 在…… …( )
在…… …( ) ,点C的坐标为
,点C的坐标为 ,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )
,点P为斜边OB上的一个动点,则PA+PC的最小值为…( )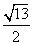 ;B.
;B. ; C.
; C. ;D.
;D. ;
;
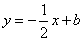 的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P
的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P 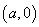 (其中
(其中 >2),过点P作x轴的垂线,分别交函数
>2),过点P作x轴的垂线,分别交函数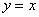 的图象于点C、D.
的图象于点C、D.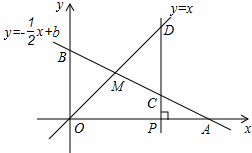 (1)求点A的坐标;
(1)求点A的坐标;