题目内容
17.下列运算正确的是( )| A. | x+x=x2 | B. | (x+y)2=x2+y2 | C. | 3x3•2x2=6a5 | D. | x8÷x2=x4 |
分析 根据单项式乘单项式的法则,完全平方公式,合并同类项的法则,同底数幂的除法的法则进行计算即可.
解答 解:A、x+x=2x,故错误;
B、(x+y)2=x2+2xy+y2,故错误;
C、3x3•2x2=6a5,故正确;
D、x8÷x2=x4故错误.
故选C.
点评 本题考查了单项式乘单项式的法则,完全平方公式,合并同类项的法则,同底数幂的除法,熟记法则是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
(1)若方程$\frac{a}{x}$-$\frac{1}{x-b}$=1(a>b)的解是x1=6,x2=10,则a=12b=5.
(2)请写出这列方程中第n个方程:$\frac{2n+4}{x}-\frac{1}{x-(n+1)}=1$ 方程的解:x1=n+2,x2=2n+2.
| 序号 | 方程 | 方程的解 |
| 1 | $\frac{6}{x}$-$\frac{1}{x-2}$=1 | x1=3,x2=4 |
| 2 | $\frac{8}{x}$-$\frac{1}{x-3}$=1 | x1=4,x2=6 |
| 3 | $\frac{10}{x}$-$\frac{1}{x-4}$=1 | x1=5,x2=8 |
| … | … | … |
(2)请写出这列方程中第n个方程:$\frac{2n+4}{x}-\frac{1}{x-(n+1)}=1$ 方程的解:x1=n+2,x2=2n+2.
6.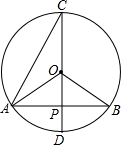 如图,⊙O中,CD是直径,且CD⊥AB于P,则下列结论中不一定正确的是( )
如图,⊙O中,CD是直径,且CD⊥AB于P,则下列结论中不一定正确的是( )
 如图,⊙O中,CD是直径,且CD⊥AB于P,则下列结论中不一定正确的是( )
如图,⊙O中,CD是直径,且CD⊥AB于P,则下列结论中不一定正确的是( )| A. | AP=PB | B. | $\widehat{AD}$=$\widehat{BD}$ | C. | ∠AOB=4∠ACD | D. | PO=PD |
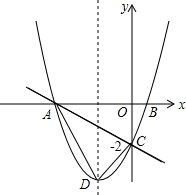 已知抛物线y=ax2+bx+c与x轴交于A、B两点,交y轴于点C,点D为顶点且△ABC的是直角三角形,A点坐标为(-4,0),C点的坐标为(0,-2),直线y=kx+b经过A、C两点.
已知抛物线y=ax2+bx+c与x轴交于A、B两点,交y轴于点C,点D为顶点且△ABC的是直角三角形,A点坐标为(-4,0),C点的坐标为(0,-2),直线y=kx+b经过A、C两点.