题目内容
 如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
解:BE∥CF.
理由:∵AB⊥BC,BC⊥CD(已知)
∴________=________=90°________
∵∠1=∠2________
∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF
∴________∥________.
∠ABC ∠BCD 垂直定义 已知 BE CF
分析:首先由已知AB⊥BC,BC⊥CD得∴∠ABC=∠BCD=90°,再由已知∠1=∠2,根据等式的性质得出∠EBC=∠BCF,从而判断BE与CF的关系.
解答:理由:∵AB⊥BC,BC⊥CD(已知)
∴∠ABC=∠BCD=90°( 垂直的定义 )
∵∠1=∠2( 已知 )
∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF
∴BE∥CF (内错角相等,两直线平行 )
故答案为:∠ABC,∠BCD,垂直定义,已知,BE∥CF.
点评:此题考查的知识点是平行线的判定,关键是由已知推出BE与CF的内错角∠EBC=∠BCF.
分析:首先由已知AB⊥BC,BC⊥CD得∴∠ABC=∠BCD=90°,再由已知∠1=∠2,根据等式的性质得出∠EBC=∠BCF,从而判断BE与CF的关系.
解答:理由:∵AB⊥BC,BC⊥CD(已知)
∴∠ABC=∠BCD=90°( 垂直的定义 )
∵∠1=∠2( 已知 )
∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF
∴BE∥CF (内错角相等,两直线平行 )
故答案为:∠ABC,∠BCD,垂直定义,已知,BE∥CF.
点评:此题考查的知识点是平行线的判定,关键是由已知推出BE与CF的内错角∠EBC=∠BCF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由.
22、如图,已知AB⊥BC,BC⊥CD,∠1=∠2.试判断BE与CF的关系,并说明你的理由. 22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.
22、如图,已知AB⊥BC,ED⊥BD,AB=CD,AC=CE.那么,AC与CE有何位置关系?说明理由.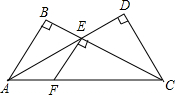 如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有:
如图,已知AB⊥BC,EF⊥BC,CD⊥AD,则有: 如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为
如图,已知AB⊥BC,AB=3,BC=4,CD=12,DA=13,四边形ABCD的面积为 如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.
如图,已知AB⊥BC于B,DC⊥BC于C,AB=DC,求证:∠1=∠2.