Question

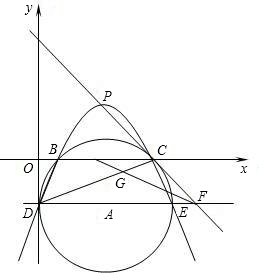如图，已知A（5，-4），⊙A与x轴分别相交于点B、C，⊙A与y轴相且于点D，
（1）求证过D、B、C三点的抛物线的解析式；
（2）连接BD，求tan∠BDC的值；
（3）点P是抛物线顶点，线段DE是直径，直线PC与直线DE相交于点F，
∠PFD的平分线FG交DC于G，求sin∠CGF的值．

Answer 1

解：（1）D（0，-4），B（2，0），C（8，0）；
∴抛物线的解析式为y=-x²+x-4
∴y=-（x-5）²+．

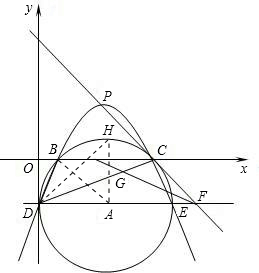
（2）由垂径定理，作弧BC的中点H，连接AH、AB，则
∠BDC=∠BAH=∠BAC，
∴tan∠BDC=tan∠BAH=．

（3）由（1）可知：P（5，），
可求得直线PC的解析式为y=-x+6．
设M为直线PC与y轴的交点，则M的坐标为（0，6）．
∴MD=MC=10，
∴∠MCD=∠MDC，
∴∠MCA=∠MDA=∠MDC+∠CDA=90°，
∴∠MCO=∠BDC=∠PFD，
∴∠CGF=∠GDF+∠PFD=∠GDF+∠BDC=∠HDF=45°，
∵DA=AH=半径，
∴sin∠CGF=sin45°=．
分析：（1）已知了A点坐标，即可得出圆的半径和OD的长，连接AB，过A作BC的垂线不难求出B、C的坐标．然后可用待定系数法求出抛物线的解析式．
（2）可取弧BC的中点H，连接AH、AB，那么根据垂径定理和圆周角定理不难得出∠BDC=∠BAC=∠BAH，由此可求出∠BDC的正切值．（也可通过求弦切角∠PCO的正切值来得出∠BDC的正切值）
（3）由于∠CGF=∠CDF+∠GFD=∠CDF+∠CFD，而∠PCO=∠PFD=∠BDC，那么∠CGF=∠CDF+∠BDC=∠HDF，在直角三角形AOH中，DA=AH，因此∠HDF=45°，即∠CGF=45°，据此可求出其正弦值．
点评：本题主要考查了二次函数解析式的确定、切线的性质、弦切角定理和垂径定理等知识．