题目内容
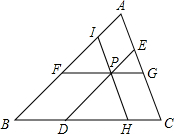如图所示．P为△ABC内一点，过P点作线段DE，FG，HI分别平行于AB，BC和CA，且DE=FG=HI=d，AB=510，BC=450，CA=425．求d．
分析：由FG∥BC，HI∥CA，ED∥AB，易证四边形AIPE、四边形BDPF、四边形CGPH均是平行四边形，利用平行线分线段成比例定理的推论可得△IHB∽△AFG∽△ABC，于是
=
，
=
，再结合
=
，先计算式子右边的和，易求
+
+
=
=2，从而有
+
+
=2，再把DE=FG=HI=d，AB=510，BC=450，CA=425代入此式，解即可．
| FG |
| BC |
| AF |
| AB |
| HI |
| CA |
| BI |
| AB |
| DE |
| AB |
| DE |
| AB |
| DE |
| AB |
| AF |
| AB |
| BI |
| AB |
| 2AB |
| AB |
| DE |
| AB |
| FG |
| BC |
| HI |
| AC |
解答：解：∵FG∥BC，HI∥CA，ED∥AB，
∴四边形AIPE、四边形BDPF、四边形CGPH均是平行四边形，
∴△IHB∽△AFG∽△ABC，
∴
=
，
=
，
∴
+
+
=
，
又∵DE=PE+PD=AI+FB，
AF=AI+FI，
BI=IF+FB，
∴DE+AF+BI=2×（AI+IF+FB）=2AB，
∴
+
+
=
=2，
∵DE=FG=HI=d，AB=510，BC=450，CA=425，
∴
+
+
=
+
+
=2，
∴
+
+
=2，
解得d=306．
解：∵FG∥BC，HI∥CA，ED∥AB，∴四边形AIPE、四边形BDPF、四边形CGPH均是平行四边形，
∴△IHB∽△AFG∽△ABC，
∴
| FG |
| BC |
| AF |
| AB |
| HI |
| CA |
| BI |
| AB |
∴
| DE |
| AB |
| AF |
| AB |
| BI |
| AB |
| DE+AF+BI |
| AB |
又∵DE=PE+PD=AI+FB，
AF=AI+FI，
BI=IF+FB，
∴DE+AF+BI=2×（AI+IF+FB）=2AB，
∴
| DE |
| AB |
| AF |
| AB |
| BI |
| AB |
| 2AB |
| AB |
∵DE=FG=HI=d，AB=510，BC=450，CA=425，
∴
| DE |
| AB |
| FG |
| BC |
| HI |
| AC |
| DE |
| AB |
| AF |
| AB |
| BI |
| AB |
∴
| d |
| 510 |
| d |
| 450 |
| d |
| 425 |
解得d=306．
点评：本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论、平行四边形的判定和性质．
练习册系列答案
相关题目
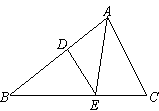
2、如图所示，D为AB边上一点，AD：DB=3：4，DE∥AC交BC于点E，则S△BDE：S△AEC等于（ ）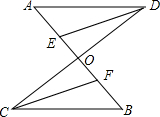
已知如图所示，O为AB、CD的中点，AE=BF，你从图中可以找到全等三角形共（ ）
