题目内容
用换元法解方程
时，如果设
，那么原方程可化为
- A.
2y2-y+1=0
- B.
2y2+y-1=0
- C.
y2-y+2=0
- D.
y2+y-2=0
B
分析：设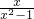
=y，再原方程中用y代替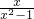，这样原方程转化为：2•y-
+1=0，然后把方程两边乘以y得到整式2y2+y-1=0．
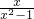解答：设=y，
原方程转化为：2•y-+1=0，
方程两边乘以y得，2y2+y-1=0．
故选B．
点评：本题考查了换元法解分式方程：用一个字母代替分式方程中某一不变的整体，使原分式方程转化为简单的分式方程或整式方程，从而达到解决原方程的目的．
分析：设
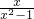=y，再原方程中用y代替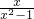，这样原方程转化为：2•y-+1=0，然后把方程两边乘以y得到整式2y2+y-1=0．解答：设
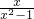=y，原方程转化为：2•y-
+1=0，方程两边乘以y得，2y2+y-1=0．
故选B．
点评：本题考查了换元法解分式方程：用一个字母代替分式方程中某一不变的整体，使原分式方程转化为简单的分式方程或整式方程，从而达到解决原方程的目的．
练习册系列答案
相关题目
时，如设
，那么将原方程化为关于
的整式方程是________________
时，如设
，那么将原方程化为关于
的整式方程是________________
时，如设
，则将原方程化为关于
的整式方程是 ．
时，如设y=x2-2x，则将原方程化为关于y的整式方程是 ．
时，如设
，则将原方程化为关于y的整式方程是 （ ）