题目内容
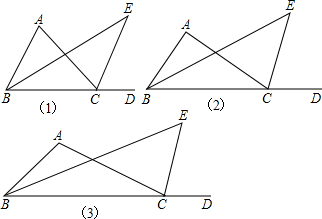 △ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
(1)如图1,若∠A=70°,求∠E的度数;
(2)如图2,若∠A=90°,求∠E的度数;
(3)如图3,若∠A=130°,求∠E的度数;
根据上述结果,你能得到什么样的一般性结论?
解:(1)∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD= ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,
∵∠ACD=∠A+∠ABC,
∴∠ECD= ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,
∴∠E=∠ECD-∠EBC= ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A,
∠A,
∵∠A=70°,
∴∠E=35°;
(2)∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD= ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,
∵∠ACD=∠A+∠ABC,
∴∠ECD= ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,
∴∠E=∠ECD-∠EBC= ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A,
∠A,
∵∠A=90°,
∴∠E=45°;
(3)∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD= ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,
∵∠ACD=∠A+∠ABC,
∴∠ECD= ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,
∴∠E=∠ECD-∠EBC= ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A,
∠A,
∵∠A=130°,
∴∠E=65°.
结论:∠E= ∠A.
∠A.
理由:∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD= ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,
∵∠ACD=∠A+∠ABC,
∴∠ECD= ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,
∴∠E=∠ECD-∠EBC= ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A.
∠A.
分析:由△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,根据角平分线的性质,可得∠ECD= ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,然后利用三角形外角的性质,即可求得:∠ECD=
∠ABC,然后利用三角形外角的性质,即可求得:∠ECD= ∠ACD=
∠ACD= ∠A+∠EBC,∠E=∠ECD-∠EBC,则可求得∠E=
∠A+∠EBC,∠E=∠ECD-∠EBC,则可求得∠E= ∠A;则可将(1)∠A=70°,(2)∠A=90°,(3)∠A=130°分别代入求解即可求得答案.
∠A;则可将(1)∠A=70°,(2)∠A=90°,(3)∠A=130°分别代入求解即可求得答案.
点评:此题考查了三角形的外角的性质与角平分线的定义.此题难度适中,解此题的关键是注意数形结合思想与整体思想的应用.
∴∠ECD=
 ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,∵∠ACD=∠A+∠ABC,
∴∠ECD=
 ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,∴∠E=∠ECD-∠EBC=
 ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A,
∠A,∵∠A=70°,
∴∠E=35°;
(2)∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD=
 ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,∵∠ACD=∠A+∠ABC,
∴∠ECD=
 ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,∴∠E=∠ECD-∠EBC=
 ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A,
∠A,∵∠A=90°,
∴∠E=45°;
(3)∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD=
 ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,∵∠ACD=∠A+∠ABC,
∴∠ECD=
 ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,∴∠E=∠ECD-∠EBC=
 ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A,
∠A,∵∠A=130°,
∴∠E=65°.
结论:∠E=
 ∠A.
∠A.理由:∵△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,
∴∠ECD=
 ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,
∠ABC,∵∠ACD=∠A+∠ABC,
∴∠ECD=
 ∠ACD=
∠ACD= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠EBC,
∠A+∠EBC,∴∠E=∠ECD-∠EBC=
 ∠A+∠EBC-∠EBC=
∠A+∠EBC-∠EBC= ∠A.
∠A.分析:由△ABC中,∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E,根据角平分线的性质,可得∠ECD=
 ∠ACD,∠EBC=
∠ACD,∠EBC= ∠ABC,然后利用三角形外角的性质,即可求得:∠ECD=
∠ABC,然后利用三角形外角的性质,即可求得:∠ECD= ∠ACD=
∠ACD= ∠A+∠EBC,∠E=∠ECD-∠EBC,则可求得∠E=
∠A+∠EBC,∠E=∠ECD-∠EBC,则可求得∠E= ∠A;则可将(1)∠A=70°,(2)∠A=90°,(3)∠A=130°分别代入求解即可求得答案.
∠A;则可将(1)∠A=70°,(2)∠A=90°,(3)∠A=130°分别代入求解即可求得答案.点评:此题考查了三角形的外角的性质与角平分线的定义.此题难度适中,解此题的关键是注意数形结合思想与整体思想的应用.

练习册系列答案
相关题目
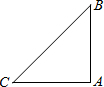 20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.
20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.