Question

【题目】定义：对于平面直角坐标系中的任意直线MN及点P，取直线MN上一点Q，线段PQ与直线MN成30°角的长度称为点P到直线MN的30°角的距离，记作d（P→MN）．
已知O为坐标原点，A（4，0），B（3，3）是平面直角坐标系中两点．根据上述定义，解答下列问题：

（1）点A到直线OB的30°角的距离d（A→OB）=；
（2）已知点G到线段OB的30°角的距离d（G→OB）=2，且点G的横坐标为1，则点G的纵坐标为 ．
（3）若点A到直线l：y=kx+1的30°角的距离d（A→l）=4，求k的值．

Answer 1

【答案】
（1）4
（2）1+ 或1﹣
（3）

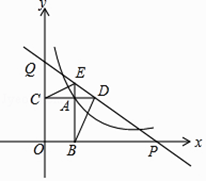
解：如图3中，作AF⊥直线l：y=kx+1于F，直线l交x轴于H，交y轴于G，设H（m，0），

易知OG=1，AE=4，AF=2，OA=4，

由△HOG∽△HFA，

∴ = ，

∴ =

解得m= 或 （舍弃），

∴H（ ，0），代入y=kx+1，得到k= = = ，

当直线l经过一、二、四象限如图所示，同法可得k=﹣ =﹣ ．

【解析】解：（1）如图1中，作AF⊥OB于F，在OB上取一点E，使得∠AEF=30°，则d（A→OB）=AE．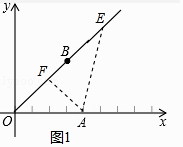

∵B（3，3），
∴∠AOF=∠OAF=45°，
∵OA=4，
∴AF=OF=2 ，
在Rt△AEF中，AE=2AF=4 ．
所以答案是4 ．（2）如图2中，作GF⊥OB于F，∠GEO=30°，GE=2，

∴FG= EG=1，
设直线x=1与直线OB交于点H，与x轴交于M，
∵∠GHF=∠HGF=45°，OM=HM=1，GF=HF=1，
∴GH= ，
∴G（1，1+ ），
当G在直线OB下方时，同法可得G′（1，1﹣ ），
所以答案是1+ 或1﹣ ．
【考点精析】关于本题考查的两点间的距离，需要了解同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记才能得出正确答案．