题目内容
已知M、N两点关于y轴对称，且点M在双曲线y=
上，点N在直线y=x+3上，设点M坐标为（a，b），则抛物线y=-abx2+（a+b）x的顶点坐标为________．
（3，
）
分析：根据点的对称性可求出ab和a+b的值，从而得出抛物线的解析式，再利用公式法可求其顶点坐标．
解答：∵M、N关于y轴对称的点，
∴纵坐标相同，横坐标互为相反数
∴点M坐标为（a，b），点N坐标为（-a，b），
∴b=
，ab=
；b=-a+3，a+b=3，则抛物线y=-abx2+（a+b）x=-x2+3x的横坐标是x=
=
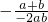=3；
纵坐标是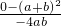
=
顶点坐标为（3，）．
点评：主要考查了二次函数的性质，函数图象上点的特征和关于坐标轴对称的点的特点．解决本题的关键是掌握好对称点的坐标规律数．
）分析：根据点的对称性可求出ab和a+b的值，从而得出抛物线的解析式，再利用公式法可求其顶点坐标．
解答：∵M、N关于y轴对称的点，
∴纵坐标相同，横坐标互为相反数
∴点M坐标为（a，b），点N坐标为（-a，b），
∴b=
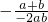，ab=；b=-a+3，a+b=3，则抛物线y=-abx2+（a+b）x=-x2+3x的横坐标是x===3；纵坐标是
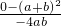=顶点坐标为（3，
）．点评：主要考查了二次函数的性质，函数图象上点的特征和关于坐标轴对称的点的特点．解决本题的关键是掌握好对称点的坐标规律数．
练习册系列答案
相关题目
已知M，N两点关于y轴对称，且点M在反比例函数y=
的图象上，点N在一次函数y=x+3的图象上，设点M的坐标为（a，b），则二次函数y=abx2+（a+b）x（ ）
| 1 |
| 2x |
A、有最小值，且最小值是
| ||
B、有最大值，且最大值是-
| ||
C、有最大值，且最大值是
| ||
D、有最小值，且最小值是-
|
已知M、N两点关于y轴对称，且点M在反比例函数y=
的图象上，点N在直线y=x+4上，设点M的坐标为（a，b），则二次函数y=-abx2+（a+b）x有（ ）
| 2 |
| x |
| A、最小值为2 |
| B、最大值为2 |
| C、最小值为-2 |
| D、最大值为-2 |