题目内容
【题目】如图1,O为正方形![]() 的中心,分别延长OA、OD到点
的中心,分别延长OA、OD到点![]() ,使OF=2OA,OE
,使OF=2OA,OE![]() ,连接EF,将
,连接EF,将![]() 绕点O按逆时针方向旋转角
绕点O按逆时针方向旋转角![]() 得到
得到![]() ,连接
,连接![]() (如图2).
(如图2).
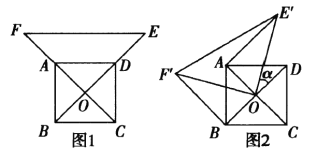
(1)探究![]() 与
与![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(2)当![]() 时,求证:
时,求证:![]() 为直角三角形.
为直角三角形.
【答案】(1)![]() ,理由见解析;(2)见解析
,理由见解析;(2)见解析
【解析】
(1)根据正方形的性质以及旋转的性质证明![]() 即可;
即可;
(2)作![]() 的中线
的中线![]() ,通过正方形的性质以及已知条件得出△AOM为等边三角形,再根据等腰三角形的性质得出
,通过正方形的性质以及已知条件得出△AOM为等边三角形,再根据等腰三角形的性质得出![]() ,从而得出
,从而得出![]() 即可.
即可.
(1)![]()
理由如下:∵O为正方形![]() 的中心,
的中心,
∴AO=DO=BO=CO,∠AOD=∠AOB=90°,
∵OF=2OA,OE![]() ,
,
∴OF=OE,
又∵![]() 是△EOF旋转得到,
是△EOF旋转得到,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴在![]() 与
与![]() 中,
中, ,
,
∴![]() (SAS)
(SAS)
∴![]() ;
;
(2)如图,作![]() 的中线
的中线![]() ,
,
则![]() ,
,
![]() ,
,
∵![]() ,
,
∴∠AOM=60°,
∴△AOM为等边三角形,
![]() ,
,
![]()
又∵![]()
![]() ,
,
![]()
即![]() ,
,
∴![]() 为直角三角形.
为直角三角形.


练习册系列答案
相关题目