题目内容
如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边a、b应满足的条件是

- A.a=
 b
b - B.a=2b
- C.a=2
 b
b - D.a=4b
B
分析:根据对折表示出小长方形的长和宽,再根据相似多边形的对应边成比例列式计算即可得解.
解答:对折两次后的小长方形的长为b,宽为 a,
a,
∵小长方形与原长方形相似,
∴ =
= ,
,
∴a=2b.
故选B.
点评:本题考查了相似多边形对应边成比例的性质,准确表示出小长方形的长和宽是解题的关键.
分析:根据对折表示出小长方形的长和宽,再根据相似多边形的对应边成比例列式计算即可得解.
解答:对折两次后的小长方形的长为b,宽为
 a,
a,∵小长方形与原长方形相似,
∴
 =
= ,
,∴a=2b.
故选B.
点评:本题考查了相似多边形对应边成比例的性质,准确表示出小长方形的长和宽是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
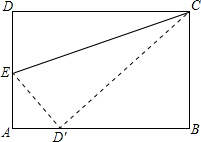 如图,取一张长方形纸片,它的长AB=10cm,宽BC=
如图,取一张长方形纸片,它的长AB=10cm,宽BC= NM与梯形BCNM的重叠面积为S,
NM与梯形BCNM的重叠面积为S,

 =______;(用含x的式子表示)
=______;(用含x的式子表示) NM与梯形BCNM的重叠面积为S,
NM与梯形BCNM的重叠面积为S,