题目内容
如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),请解答下列问题:
(1)求抛物线的解析式;
(2)抛物线的顶点为点D,对称轴与x轴交于点E,连接BD,求BD的长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣ ,
, ).
).

解:(1)∵抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),
∴将A与B坐标代入得: ,
,
解得: ,
,
则抛物线解析式为y=﹣x2+2x+3;
(2)点D为抛物线顶点,由顶点坐标(﹣ ,
, )得,D(1,4),
)得,D(1,4),
∵对称轴与x轴交于点E,
∴DE=4,OE=1,
∵B(﹣1,0),
∴BO=1,
∴BE=2,
在Rt△BED中,根据勾股定理得:BD= =
= =2
=2 .
.

练习册系列答案
相关题目

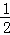 ,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(
,且经过点(2,0),下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(﹣2,y1),(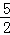 ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )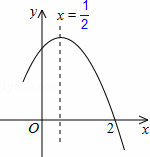

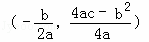 ].
].
 时,甲车刚好行驶80千米.求此时乙车到达A地还需行驶多长时间.
时,甲车刚好行驶80千米.求此时乙车到达A地还需行驶多长时间.