题目内容
1.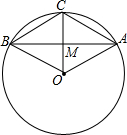 在⊙O,∠AOM=60°,C为$\widehat{AB}$的中点,AB、OC交于点M,试判断四边形OABC的形状,并说明理由.
在⊙O,∠AOM=60°,C为$\widehat{AB}$的中点,AB、OC交于点M,试判断四边形OABC的形状,并说明理由.
分析 先判断△OAC为等边三角形得到AC=OA,再利用圆心角、弧、弦的关系,由$\widehat{AC}$=$\widehat{BC}$得到∠BOC=∠AOC=60°,又可判定△OBC为等边三角形,则BC=OB,所以OB=BC=CA=OA,于是可判断四边形OABC为菱形.
解答 解:四边形OABC为菱形.理由如下:
∵OC=OA,∠AOM=60°,
∴△OAC为等边三角形,
∴AC=OA,
∵C为$\widehat{AB}$的中点,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠BOC=∠AOC=60°,
同理可得△OBC为等边三角形,
∴BC=OB,
即OB=BC=CA=OA,
∴四边形OABC为菱形.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等边三角形的判定与性质和菱形的判定方法.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 在一个三角形中最多有两个锐角 | B. | 在一个三角形中最多有两个钝角 | ||
| C. | 在一个三角形中最多有两个直角 | D. | 在一个三角形中最少有两个锐角 |
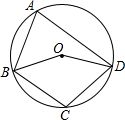 如图,A、B、C、D四点都在⊙O上,∠C=100°,则:
如图,A、B、C、D四点都在⊙O上,∠C=100°,则: