题目内容
 如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的
如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的
是________.
①P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.
①②③④
分析:首先根据角平分线上点的性质,推出①正确,然后通过求证△ARP和△ASP全等,推出②正确,再根据AQ=PQ,推出相关角相等,通过等量代换即可得∠QPA=∠QAR,即可推出③正确,依据等边三角形的性质和外角的性质推出∠PQS=∠B,便可推出结论④.
解答:∵PR=PS,PR⊥AB,PS⊥AC,
∴P在∠A的平分线上,
在Rt△ARP和Rt△ASP中,
∵ ,
,
∴Rt△ARP≌Rt△ASP(HL),
∴AS=AR,∠QAP=∠PAR,
∵AQ=PQ,
∴∠PAR=∠QPA,
∴∠QPA=∠QAR
∴QP∥AR,
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∴∠PAR=∠QPA=30°,
∴∠PQS=60°,
在△BRP和△QSP中,
∵ ,
,
∴△BRP≌△QSP(AAS),
∴①②③④项四个结论都正确,
故答案为①②③④.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质、等边对等角,直角三角形的性质,平行线的判定,关键在于熟练运用等边三角形的性质、全等三角形的判定定理,认真推理计算相关的等量关系.
分析:首先根据角平分线上点的性质,推出①正确,然后通过求证△ARP和△ASP全等,推出②正确,再根据AQ=PQ,推出相关角相等,通过等量代换即可得∠QPA=∠QAR,即可推出③正确,依据等边三角形的性质和外角的性质推出∠PQS=∠B,便可推出结论④.
解答:∵PR=PS,PR⊥AB,PS⊥AC,
∴P在∠A的平分线上,
在Rt△ARP和Rt△ASP中,
∵
 ,
,∴Rt△ARP≌Rt△ASP(HL),
∴AS=AR,∠QAP=∠PAR,
∵AQ=PQ,
∴∠PAR=∠QPA,
∴∠QPA=∠QAR
∴QP∥AR,
∵△ABC为等边三角形,
∴∠B=∠C=∠BAC=60°,
∴∠PAR=∠QPA=30°,
∴∠PQS=60°,
在△BRP和△QSP中,
∵
 ,
,∴△BRP≌△QSP(AAS),
∴①②③④项四个结论都正确,
故答案为①②③④.
点评:本题主要考查等边三角形的性质、全等三角形的判定与性质、等边对等角,直角三角形的性质,平行线的判定,关键在于熟练运用等边三角形的性质、全等三角形的判定定理,认真推理计算相关的等量关系.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
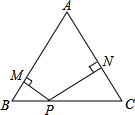 如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )A、
| ||||||
B、
| ||||||
C、80%<
| ||||||
D、78%<
|
 AE=120°,试问:
AE=120°,试问: 附加题.观察计算
附加题.观察计算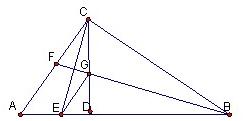 如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分.
如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分. 如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=
如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=