题目内容
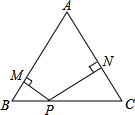 如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )A、
| ||||||
B、
| ||||||
C、80%<
| ||||||
D、78%<
|
分析:设BM=x,CN=y,用x、y分别表示m、n的值,化简m、n的表达式,可得四边形AMPN,△ABC的周长的比值,可以解题.
解答:解:设BM=x,CN=y
则BP=2x,PC=2y,PM=
x,PN=
y
AM+AN=2BC-(BM+CN)=3(x+y),
故
=
=
≈0.7887.
故选D.
则BP=2x,PC=2y,PM=
| 3 |
| 3 |
AM+AN=2BC-(BM+CN)=3(x+y),
故
| m |
| n |
(3 +
| ||
| 3×2(x+y) |
=
3+
| ||
| 6 |
故选D.
点评:本题考查了等边三角形各内角为60°的性质,等边三角形周长的计算,本题中用x、y表示m、n的值是解题的关键.

练习册系列答案
相关题目
 AE=120°,试问:
AE=120°,试问: 附加题.观察计算
附加题.观察计算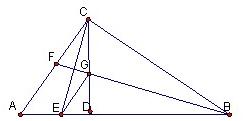 如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分.
如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分. 如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=
如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=