题目内容
 己知二次函数
己知二次函数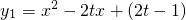 (t>1)的图象为抛物线C1.
(t>1)的图象为抛物线C1.
(1)求证:无论t取何值,抛物线C1与y轴总有两个交点;
(2)已知抛物线C1与x轴交于A、B两点(A在B的左侧),将抛物线C1作适当的平移,得抛物线C2: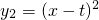 ,平移后A、B的对应点分别为D(m,n),E(m+2,n),求n的值.
,平移后A、B的对应点分别为D(m,n),E(m+2,n),求n的值.
(3)在(2)的条件下,将抛物线C2位于直线DE下方的部分沿直线DE向上翻折后,连同C2在DE上方的部分组成一个新图形,记为图形G,若直线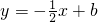 (b<3)与图形G有且只有两个公共点,请结合图象求b的取值范围.
(b<3)与图形G有且只有两个公共点,请结合图象求b的取值范围.
解:(1)令y1=0,得△=(-2t)2-4(2t-1)=4t2-8t+4=4(t-1)2,
∵t>1,∴△=4(t-1)2>0,
∴无论t取何值,方程x2-2tx+(2t-1)=0总有两个不相等的实数根,
∴无论t取何值,抛物线C1与y轴总有两个交点.
(2)解方程x2-2tx+(2t-1)=0得,x1=1,x2=2t-1,
∵t>1,∴2t-1>1.得A(1,0),B(2t-1,0),
∵D(m,n),E(m+2,n),∴DE=AB=2,
即2t-1-1=2,解得t=2.
∴二次函数为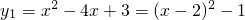 ,
,
显然将抛物线C1向上平移1个单位可得抛物线C2: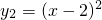 ,
,
故n=1.
(3)由(2)得抛物线C2: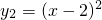 ,D(1,1),E(3,1),
,D(1,1),E(3,1),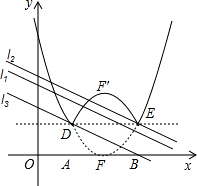
翻折后,顶点F(2,0)的对应点为F'(2,2),
如图,当直线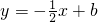 经过点D(1,1)时,记为l1,
经过点D(1,1)时,记为l1,
此时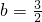 ,图形G与l1只有一个公共点;
,图形G与l1只有一个公共点;
当直线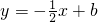 经过点E(3,1)时,记为l2,此时
经过点E(3,1)时,记为l2,此时 ,图形G与l2有三个公共点;
,图形G与l2有三个公共点;
当b<3时,由图象可知,只有当直线l: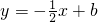 位于l1与l2之间时,图形G与直线l有且只有两个公共点,
位于l1与l2之间时,图形G与直线l有且只有两个公共点,
∴符合题意的b的取值范围是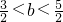 .
.
分析:(1)求出b2-4ac的值,根据根的判别式为正数即可得到答案;
(2)首先用含有t的字母表示出点A与点B的坐标,然后根据点D和点E的坐标得到DE=AB=2,从而求得t值,配方后利用平移规律得到平移个数即可;
(3)分三种情况讨论后即可求得变量t的取值范围.
点评:本题主要考查对二次函数图象上点的坐标特征,根与系数的关系,解一元二次方程,平移的性质等知识点的理解和掌握,能根据性质进行推理是解此题的关键.
∵t>1,∴△=4(t-1)2>0,
∴无论t取何值,方程x2-2tx+(2t-1)=0总有两个不相等的实数根,
∴无论t取何值,抛物线C1与y轴总有两个交点.
(2)解方程x2-2tx+(2t-1)=0得,x1=1,x2=2t-1,
∵t>1,∴2t-1>1.得A(1,0),B(2t-1,0),
∵D(m,n),E(m+2,n),∴DE=AB=2,
即2t-1-1=2,解得t=2.
∴二次函数为
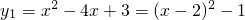 ,
,显然将抛物线C1向上平移1个单位可得抛物线C2:
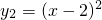 ,
,故n=1.
(3)由(2)得抛物线C2:
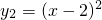 ,D(1,1),E(3,1),
,D(1,1),E(3,1),
翻折后,顶点F(2,0)的对应点为F'(2,2),
如图,当直线
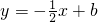 经过点D(1,1)时,记为l1,
经过点D(1,1)时,记为l1,此时
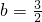 ,图形G与l1只有一个公共点;
,图形G与l1只有一个公共点;当直线
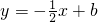 经过点E(3,1)时,记为l2,此时
经过点E(3,1)时,记为l2,此时 ,图形G与l2有三个公共点;
,图形G与l2有三个公共点;当b<3时,由图象可知,只有当直线l:
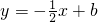 位于l1与l2之间时,图形G与直线l有且只有两个公共点,
位于l1与l2之间时,图形G与直线l有且只有两个公共点,∴符合题意的b的取值范围是
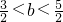 .
.分析:(1)求出b2-4ac的值,根据根的判别式为正数即可得到答案;
(2)首先用含有t的字母表示出点A与点B的坐标,然后根据点D和点E的坐标得到DE=AB=2,从而求得t值,配方后利用平移规律得到平移个数即可;
(3)分三种情况讨论后即可求得变量t的取值范围.
点评:本题主要考查对二次函数图象上点的坐标特征,根与系数的关系,解一元二次方程,平移的性质等知识点的理解和掌握,能根据性质进行推理是解此题的关键.

练习册系列答案
相关题目
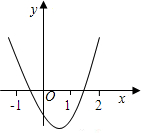 己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)a-b+c>0
(2)方程ax2+bx+c=0两根之和大于零
(3)y随x的增大而增大
(4)一次函数y=x+bc的图象一定不过第四象限.其中正确的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
己知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: (2013•燕山区一模)己知二次函数
(2013•燕山区一模)己知二次函数 (2013•松北区三模)如图,己知二次函数y=-
(2013•松北区三模)如图,己知二次函数y=-