题目内容
【题目】△ ![]() 中,
中, ![]() .取
.取 ![]() 边的中点
边的中点 ![]() ,作
,作 ![]() ⊥
⊥ ![]() 于点
于点 ![]() ,取
,取 ![]() 的中点
的中点 ![]() ,连接
,连接 ![]() ,
, ![]() 交于点
交于点 ![]() .
.
(1)如图1,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并求
并求 ![]() 的值;
的值;
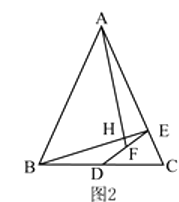
(2)如图2,如果 ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() 并用含
并用含 ![]() 的式子表示
的式子表示 ![]() .
.
【答案】
(1)解:如图1,连接AD,
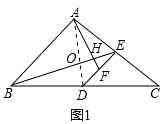
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC= ![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,∴ ![]() ,即ADCE=BDDE.
,即ADCE=BDDE.
∵点D是BC的中点,点F是DE的中点,
∴BD= ![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═ ![]() BC2DF=BCDF,
BC2DF=BCDF,
∴ ![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴ ![]() ,在Rt△ADB中,
,在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°- ![]() ∠BAC,BD=
∠BAC,BD= ![]() BC,
BC,
∴tan∠ABD=tan(90°- ![]() ∠BAC)=
∠BAC)= ![]() ,
,
∴ ![]() =
= ![]() tan(90°-
tan(90°- ![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°
根据以上结论可得:∠AHB=90°, ![]() =
= ![]() tan(90°-
tan(90°- ![]() ×90°)=
×90°)= ![]() ;∴AF⊥BE,
;∴AF⊥BE, ![]() =
= ![]()
(2)解:如图2,
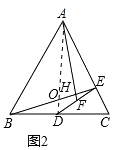
根据以上结论可得:∠AHB=90°, ![]() =
= ![]() tan(90°-
tan(90°- ![]() α);∴AF⊥BE, =
α);∴AF⊥BE, = ![]() tan(90°-
tan(90°- ![]() α)
α)
【解析】(1)由AB=AC,点D是BC的中点,根据三线合一,得到AD⊥BC,由DE⊥AC,根据同角的余角相等,得到∠ADE=∠C;得到△ADB∽△DEC,得到比例,即ADCE=BDDE;由已知得到ADCE=BCDF,又∠ADE=∠C,得到△AFD∽△BEC,得到比例,在Rt△ADB中,根据三角函数定义,得到∠DAF=∠CBE,由三角形内角和定理求出∠AHO=90°,即∠AHB=90°,根据以上结论可得![]()
【考点精析】掌握相似三角形的判定与性质和锐角三角函数的定义是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

 阅读快车系列答案
阅读快车系列答案