Question

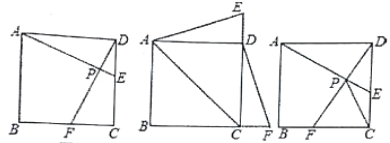
【题目】如图，在等边 中， ， ， 分别是 ， ， 上的点， ， ， ，则 的面积与 的面积之比等于（ ）

A.1∶3
B.2∶3
C. ∶2
D. ∶3

Answer 1

【答案】A
【解析】∵DE⊥AC，EF⊥AB，FD⊥BC，

∴∠C+∠EDC=90°，∠FDE+∠EDC=90°，

∴∠C=∠FDE，

同理可得：∠B=∠DFE，∠A=DEF，

∴△DEF∽△CAB，

∴△DEF与△ABC的面积之比= ，

又∵△ABC为正三角形，

∴∠B=∠C=∠A=60°

∴△EFD是等边三角形，

∴EF=DE=DF，

又∵DE⊥AC，EF⊥AB，FD⊥BC，

∴△AEF≌△CDE≌△BFD，

∴BF=AE=CD，AF=BD=EC，

在Rt△DEC中，

DE=DC×sin∠C= DC，EC=cos∠C×DC= DC，

又∵DC+BD=BC=AC= DC，

∴ ，

∴△DEF与△ABC的面积之比等于：

所以答案是：A．

【考点精析】掌握相似三角形的判定与性质和解直角三角形是解答本题的根本，需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．