Question

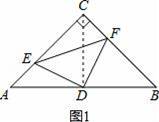
如图，在△ABC中，∠C=90°，AC=BC=2，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CEDF的周长不变；③点C到线段EF的最大距离为1．其中正确的结论有　　．（填写所有正确结论的序号）

Answer 1

①③【考点】全等三角形的判定与性质；等腰直角三角形．

【分析】①作常规辅助线连接CD，由SAS定理可证△CDF和△ADE全等，从而可证∠EDF=90°，DE=DF．所以△DFE是等腰直角三角形；

②当E、F分别为AC、BC中点时，EF取最小值，得到EF的值是变化的，DE和DF也是变化的，于是四边形CEDF的周长变，不正确，

③△DEF是等腰直角三角形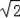， DE=EF，当DF与BC垂直，即DF最小时，FE取最小值2，此时点C到线段EF的最大距离是1．

【解答】解：①连接CD；

∵△ABC是等腰直角三角形，

∴∠DCB=∠A=45°，CD=AD=DB；

∵AE=CF，

∴△ADE≌△CDF（SAS）；

∴ED=DF，∠CDF=∠EDA；

∵∠ADE+∠EDC=90°，

∴∠EDC+∠CDF=∠EDF=90°，

∴△DFE是等腰直角三角形．

∴①正确；

②当E、F分别为AC、BC中点时，EF取最小值，

∴EF的值是变化的，

∴DE和DF也是变化的，

∴四边形CEDF的周长变，

∴②不正确，

③△DEF是等腰直角三角形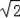， DE=EF，

当EF∥AB时，∵AE=CF，

∴E，F分别是AC，BC的中点，故EF是△ABC的中位线，

∴EF取最小值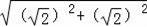=2，

∵CE=CF=，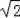

∴此时点C到线段EF的最大距离=EF=1，

∴③正确，

故答案为：①③

【点评】此题主要考查了全等三角形的判定与性质以及正方形、等腰三角形、直角三角形性质等知识，找到EF∥BC时取最小值是解题关键．