Question

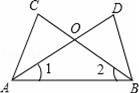
如图，△ABC与△ABD中，AD与BC相交于O点，∠1=∠2，请你添加一个条件（不再添加其它线段，不再标注或使用其他字母），使AC=BD，并给出证明．

你添加的条件是：　 　．

证明：　 　．

Answer 1

【考点】全等三角形的判定与性质．

【分析】要使AC=BD，可以证明△ACB≌△BDA或者△ACO≌△BDO从而得到结论．

【解答】解：添加条件例举：AD=BC；OC=OD；∠C=∠D；∠CAO=∠DBC等．

证明：（1）如果添加条件是AD=BC时，

∵BC=AD，∠2=∠1，AB=BA，

在△ABC与△BAD中，

，

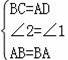
∴△ABC≌△BAD，

∴AC=BD；

（2）如果添加条件是OC=OD时，

∵∠1=∠2

∴OA=OB

∴OA+OD=OB+OD

∴BC=AD

又∵∠2=∠1，AB=BA

在△ABC与△BAD中，，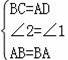

∴△ABC≌△BAD，

∴AC=BD；

（3）如果添加条件是∠C=∠D时，

∵∠2=∠1，AB=BA，

在△ABC与△BAD中，

，

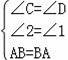
∴△ABC≌△BAD，

∴AC=BD；

（4）如果添加条件是∠CAO=∠DBC时，

∵∠1=∠2，

∴∠CAO+∠1=∠DBC+∠2，

∴∠CAB=∠DBA，

又∵AB=BA，∠2=∠1，

在△ABC与△BAD中，，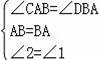

∴△ABC≌△BAD，

∴AC=BD．

故答案为：AD=BC；OC=OD；∠C=∠D；∠CAO=∠DBC．

【点评】本题考查了全等三角形的判定及性质；判定两个三角形全等的方法有：SSS，SAS，ASA，AAS，本题已知一边一角，所以可以寻找夹这个角的另外一边或者是另外两个角．