题目内容
5. 在Rt△ABC中,∠ABC=90°,∠C=30°,AB=4cm,若点E为Rt△ABC斜边AC上一动点,过点E作EF⊥AC,交直线AB于点F,将△AEF沿EF折叠,其中点A的对应点为A′,若使△A′BC为等腰三角形,则AE的长为2cm或(4-2$\sqrt{3}$)cm或(4+2$\sqrt{3}$)cm.
在Rt△ABC中,∠ABC=90°,∠C=30°,AB=4cm,若点E为Rt△ABC斜边AC上一动点,过点E作EF⊥AC,交直线AB于点F,将△AEF沿EF折叠,其中点A的对应点为A′,若使△A′BC为等腰三角形,则AE的长为2cm或(4-2$\sqrt{3}$)cm或(4+2$\sqrt{3}$)cm.
分析 解直角三角形得到∠A=60°,AC=8cm,BC=4$\sqrt{3}$cm,①当A′B=A′C时,如图1,推出△AA′B是等边三角形,于是得到AA′=4cm,根据折叠的性质即可得到AE=$\frac{1}{2}$A′A=2cm;②当A′C=BC=4$\sqrt{3}$cm时,如图2,由线段的和差得到AA′=8-4$\sqrt{3}$,求得AE=$\frac{1}{2}$AA′=(4-2$\sqrt{3}$)cm,AE=$\frac{1}{2}$AA″=(4+2$\sqrt{3}$)cm;③当A′B=BC时,这种情况不存在.
解答 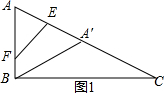 解:∵∠ABC=90°,∠C=30°,
解:∵∠ABC=90°,∠C=30°,
∴∠A=60°,∵AB=4cm,
∴AC=8cm,BC=4$\sqrt{3}$cm,
①当A′B=A′C时,如图1,
∵∠AA′B=∠A′BC+∠C=60°,
∴∠A=∠AA′B,
∴△AA′B是等边三角形,
∴AA′=A′B=A′C=$\frac{1}{2}$AC,
∴AA′=4cm,
∵将△AEF沿EF折叠,其中点A的对应点为A′,
∴AE=$\frac{1}{2}$A′A=2cm;
②当A′C=BC=4$\sqrt{3}$cm时,如图2,
∵AC=8cm,
∴AA′=8-4$\sqrt{3}$,
∴AE=$\frac{1}{2}$AA′=(4-2$\sqrt{3}$)cm,
∵A″C=BC=4$\sqrt{3}$,
∴AA′=(8+4$\sqrt{3}$)cm,
∴AE=$\frac{1}{2}$AA′=(4+2$\sqrt{3}$)cm;
③当A′B=BC时,这种情况不存在,
∴若使△A′BC为等腰三角形,则AE的长为2cm或(4-2$\sqrt{3}$)cm或(4+2$\sqrt{3}$)cm.
故答案为:2cm或(4-2$\sqrt{3}$)cm或(4+2$\sqrt{3}$)cm.
点评 本题考查了翻折变换-折叠问题,等腰三角形的判定,含30°角的直角三角形的性质,正确的作出图形是解题的关键.

 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,则不等式kx+b<$\frac{m}{x}$的解集是( )
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,则不等式kx+b<$\frac{m}{x}$的解集是( )| A. | x>1或-2<x<0 | B. | x<-2或0<x<1 | C. | -2<x<1 | D. | x>1或x<-2 |
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
| A. | 8的立方根是2 | B. | -8的立方根是-2 | ||
| C. | 0的立方根是0 | D. | $\root{3}{{a}^{2}}$的立方根是a2 |
 已知:如图,正方形ABCD,DE⊥MF,求证:BM+CF=CE.
已知:如图,正方形ABCD,DE⊥MF,求证:BM+CF=CE. 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC,DA平分∠BDE.
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC,DA平分∠BDE. 如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.
如图,在四边形ABCD中,AB∥DC,E是AD中点,EF⊥BC于点F,BC=5,EF=3.