题目内容
如果a、b、c为互不相等的实数,且满足关系式b2+c2=2a2+16a+14与bc=a2-4a-5,那么a的取值范围是
- A.-1<a<5
- B.a>-1
- C.a<-7或a>-1
- D.a<-1或a>5
B
分析:根据b,c关系就可以得到含有a的不等式,b2+c2>0即2a2+16a+14>0;bc≤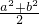 ,则2a2+16a+14≥2(a2-4a-5),解这两个关于a的不等式组成的不等式组就可以求出a的范围.
,则2a2+16a+14≥2(a2-4a-5),解这两个关于a的不等式组成的不等式组就可以求出a的范围.
解答:∵b不等于c,
∴b2+c2>0,即2a2+16a+14>0,即:2(a+7)(a+1)>0,
解得a<-7或a>-1.
又∵b2+c2=2a2+16a+14,bc=a2-4a-5,
b2+c2>2bc,
即2a2+16a+14>2(a2-4a-5),
24a>-24,
a>-1.
综上所述,a的取值范围是a>-1.
故选:B.
点评:此题主要考查了利用不等式的性质以及完全平方公式的应用,利用(b-c)2≥0,可得到b2+c2≥2bc.通过b,c的关系,转化为含a的不等式是解决本题的关键.
分析:根据b,c关系就可以得到含有a的不等式,b2+c2>0即2a2+16a+14>0;bc≤
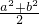 ,则2a2+16a+14≥2(a2-4a-5),解这两个关于a的不等式组成的不等式组就可以求出a的范围.
,则2a2+16a+14≥2(a2-4a-5),解这两个关于a的不等式组成的不等式组就可以求出a的范围.解答:∵b不等于c,
∴b2+c2>0,即2a2+16a+14>0,即:2(a+7)(a+1)>0,
解得a<-7或a>-1.
又∵b2+c2=2a2+16a+14,bc=a2-4a-5,
b2+c2>2bc,
即2a2+16a+14>2(a2-4a-5),
24a>-24,
a>-1.
综上所述,a的取值范围是a>-1.
故选:B.
点评:此题主要考查了利用不等式的性质以及完全平方公式的应用,利用(b-c)2≥0,可得到b2+c2≥2bc.通过b,c的关系,转化为含a的不等式是解决本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目