题目内容
5. 如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,连结OD、AD,则以下结论:①D是BC的中点;②AD⊥BC;③AD是∠BAC的平分线;④OD∥AC.其中正确结论的个数为( )
如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,连结OD、AD,则以下结论:①D是BC的中点;②AD⊥BC;③AD是∠BAC的平分线;④OD∥AC.其中正确结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由AB=AC,得到∠B=∠C,由于AB为⊙O的直径,得到AD⊥BC,根据相似三角形的性质得到①②③正确,由于OB=OD,于是得到∠B=∠ODB,根据同位角相等,两直线平行即可得到④正确.
解答 解:∵AB=AC,
∴∠B=∠C,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∴BD=CD,∠BAD=∠CAD,
∴D是BC的中点,AD是∠BAC的平分线,
∴①②③正确,
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴④正确,
故选D.
点评 本题考查了等腰三角形的判定与性质,圆周角定理,平行线的判定,熟练掌握等腰三角形的性质-三线合一是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
14.如果x-$\frac{1}{x}$=3,则${x^2}+\frac{1}{x^2}$的值为( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
15.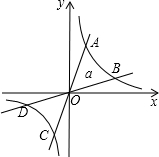 如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
 如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )
如图,直线L与双曲线交于A、C两点,将直线L绕点O顺时针旋转α度角(0°<α≤45°),与双曲线交于B、D两点,则四边形ABCD形状一定是( )| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
 如图,过双曲线y=$\frac{8}{x}$(x>0)上三点B1、B2、B3分别作坐标轴的垂线段,且OA1=A1A2=A2A3,连结OB1、OB2、OB3,则图中阴影部分的面积是$\frac{49}{9}$.
如图,过双曲线y=$\frac{8}{x}$(x>0)上三点B1、B2、B3分别作坐标轴的垂线段,且OA1=A1A2=A2A3,连结OB1、OB2、OB3,则图中阴影部分的面积是$\frac{49}{9}$.