题目内容
20.如图1,AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,连AC.(1)求证:AC平分∠DAB;
(2)如图2,延长AB,交直线DC于E,若$\frac{AD}{AB}$=$\frac{4}{5}$,求tan∠E.

分析 (1)连结OC,如图1,根据切线的性质得OC⊥CD,而AD⊥CD,所以OC∥AD,根据平行线的性质得∠1=∠2,加上∠1=∠2,所以∠2=∠3,于是可判断AC平分∠DAB;
(2)连结OC,如图2,由$\frac{AD}{AB}$=$\frac{4}{5}$,可设AD=4x,AB=5x,则OC=OA=$\frac{5}{2}$x,接着证明△EOC∽△EAD,利用相似比可计算出EO=$\frac{25}{6}$x,然后在Rt△OCE中,根据勾股定理计算出CE=$\frac{10}{3}$x,再利用正切定义求解.
解答 (1)证明: 连结OC,如图1,
连结OC,如图1,
∵CD为⊙O的切线,
∴OC⊥CD,
而AD⊥CD,
∴OC∥AD,
∴∠1=∠2,
∵OA=OC,
∴∠1=∠2,
∴∠2=∠3,
∴AC平分∠DAB;
(2)解:连结OC,如图2, 由$\frac{AD}{AB}$=$\frac{4}{5}$,可设AD=4x,AB=5x,则OC=OA=$\frac{5}{2}$x,
由$\frac{AD}{AB}$=$\frac{4}{5}$,可设AD=4x,AB=5x,则OC=OA=$\frac{5}{2}$x,
∵OC∥AD,
∴△EOC∽△EAD,
∴$\frac{OC}{AD}$=$\frac{EO}{EA}$,即$\frac{\frac{5}{2}x}{4x}$=$\frac{EO}{EO+\frac{5}{2}x}$,解得EO=$\frac{25}{6}$x,
在Rt△OCE中,CE=$\sqrt{O{E}^{2}-O{C}^{2}}$=$\sqrt{(\frac{25}{6}x)^{2}-(\frac{5}{2}x)^{2}}$=$\frac{10}{3}$x,
∴tanE=$\frac{OC}{CE}$=$\frac{\frac{5}{2}x}{\frac{10}{3}x}$=$\frac{3}{4}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质和解直角三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,连结OD、AD,则以下结论:①D是BC的中点;②AD⊥BC;③AD是∠BAC的平分线;④OD∥AC.其中正确结论的个数为( )
如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,连结OD、AD,则以下结论:①D是BC的中点;②AD⊥BC;③AD是∠BAC的平分线;④OD∥AC.其中正确结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 成绩 | 45 | 46 | 47 | 48 | 49 | 50 |
| 人数 | 1 | 1 | 4 | 2 | 5 | 2 |
| A. | 47,49 | B. | 47,50 | C. | 48,49 | D. | 48,50 |
 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点. 如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,问:∠EDF与∠EFD是否相等?并说明理由.
如图,在△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,问:∠EDF与∠EFD是否相等?并说明理由.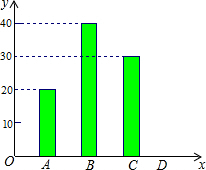 “五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题:
“五•一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.如图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题: