题目内容
【题目】探究：
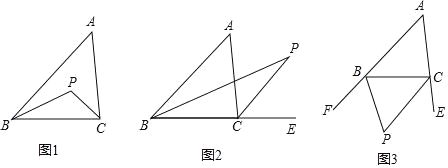
（1）如图1，在△ABC中，BP平分∠ABC，CP平分∠ACB．求证：∠P＝90°+
∠A．
（2）如图2，在△ABC中，BP平分∠ABC，CP平分外角∠ACE．猜想∠P和∠A有何数量关系，并证明你的结论．
（3）如图3，BP平分∠CBF，CP平分∠BCE．猜想∠P和∠A有何数量关系，请直接写出结论．
【答案】（1）见解析；（2）
∠A＝∠P，理由见解析；（3）∠P＝90°﹣∠A，理由见解析
【解析】
（1）根据三角形内角和定理以及角平分线的性质进行解答即可：
（2）根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和，可求出∠A的度数，根据补角的定义求出∠ACB的度数，根据三角形的内角和即可求出∠P的度数，即可求出结果，
（3）根据三角形的外角性质、内角和定理、角平分线的定义探求并证明.
证明：（1）∵△ABC中，∠ABC+∠ACB＝180°﹣∠A．
又∵BP平分∠ABC，CP平分∠ACB，
∴∠PBC＝∠ABC，
∠PCB＝∠ACB，
∴∠PBC+∠PCB＝（180°﹣∠A），
根据三角形内角和定理可知∠BPC＝180°﹣（180°﹣∠A）＝90°+∠A；
（2）∠A＝∠P，理由如下：
∵BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，
∴∠PBC＝∠ABC，∠PCE＝∠ACE．
∵∠ACE是△ABC的外角，∠PCE是△BPC的外角，
∴∠ACE＝∠ABC+∠A，∠PCE＝∠PBC+∠P，
∴∠ACP＝∠ABC+∠A，
∴∠ABC+∠A＝∠PBC+∠P，
∴∠A＝∠P．
（3）∠P＝90°﹣∠A，理由如下：
∵P点是外角∠CBF和∠BCE的平分线的交点，∠P+∠PBC+∠PCB＝180°
∴∠P＝180°﹣（∠PBC+∠PCB）
＝180°﹣（∠FBC+∠ECB）
＝180°﹣（∠A+∠ACB+∠A+∠ABC）
＝180°﹣（∠A+180°）
＝90°﹣∠A．
