题目内容
 点B与点P都在反比例函数y=
点B与点P都在反比例函数y=| k |
| x |
(1)求反比函数的解析式;
(2)求S与m的函数关系.
考点:反比例函数综合题
专题:代数综合题
分析:(1)利用OB=4,∠BOA=30°求得线段AB和线段OA的长即可得到点B的坐标,进而可以求得经过点B的双曲线的解析式;
(2)当P点在B点左边时,求得线段OB所在直线的解析式,然后求得线段OB和线段PC的交点坐标,进而可以表示出面积S,当P点在B点右边时,求出AD的长,进而得出S.
(2)当P点在B点左边时,求得线段OB所在直线的解析式,然后求得线段OB和线段PC的交点坐标,进而可以表示出面积S,当P点在B点右边时,求出AD的长,进而得出S.
解答:解:(1)∵OB=4,过B,P作x轴垂线垂足分别为A,C,∠BOA=30°,
∴BA=
OB=2,
∴OA=
AB=2
,
∴点B的坐标为:(2
,2),
∵点B在反比例函数y=
(k>0)(x>0)第一象限的图象上,
∴2=
,
解得:k=4
,
∴反比例函数的解析式为:y=
;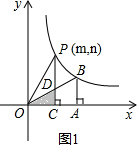
(2)如图1,当P点在B点左边时,
设线段OB所在直线的解析式为:y=kx,
∵y=kx经过B点,
∴2
k=2,
解得:k=
,
∴线段OB所在直线的解析式为:y=
x.
∵P点的坐标为(m,n),PC⊥x轴于点C,
∴D点的横坐标为m,
∵点D在直线:y=
x上,
∴点D的纵坐标为
m,
∴线段OC=m,线段CD=
m,
∴S=
OC•CD=
×m×
m=
m2.
如图2,当P点在B点右边时,
∵P点的坐标为(m,n),且在反比例函数y=
上,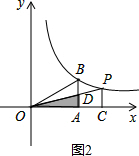
∴P点坐标为:(m,
),
∵AD∥PC,
∴△OAD∽△OCP,
∴
=
,
∴
=
,
∴AD=
,
∴S=
OA•AD=
×2
×
=
.
∴BA=
| 1 |
| 2 |
∴OA=
| 3 |
| 3 |
∴点B的坐标为:(2
| 3 |
∵点B在反比例函数y=
| k |
| x |
∴2=
| k | ||
2
|
解得:k=4
| 3 |
∴反比例函数的解析式为:y=
4
| ||
| x |

(2)如图1,当P点在B点左边时,
设线段OB所在直线的解析式为:y=kx,
∵y=kx经过B点,
∴2
| 3 |
解得:k=
| ||
| 3 |
∴线段OB所在直线的解析式为:y=
| ||
| 3 |
∵P点的坐标为(m,n),PC⊥x轴于点C,
∴D点的横坐标为m,
∵点D在直线:y=
| ||
| 3 |
∴点D的纵坐标为
| ||
| 3 |
∴线段OC=m,线段CD=
| ||
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
如图2,当P点在B点右边时,
∵P点的坐标为(m,n),且在反比例函数y=
4
| ||
| x |

∴P点坐标为:(m,
4
| ||
| m |
∵AD∥PC,
∴△OAD∽△OCP,
∴
| AO |
| CO |
| AD |
| PC |
∴
2
| ||
| m |
| AD | ||||
|
∴AD=
| 24 |
| m2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 24 |
| m2 |
24
| ||
| m2 |
点评:本题考查了反比例函数的综合知识,解题的关键是能够将点的坐标转化为线段的长,从而用点的坐标表示出三角形的面积.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
满足
+
=
的整数对(a,b)的个数是( )
| a |
| b |
| 275 |
| A、8 | B、6 | C、4 | D、3 |
 不在同一直线上的三点A、B、C,如图所示,以这三点为顶点作平行四边形,最多能作( )
不在同一直线上的三点A、B、C,如图所示,以这三点为顶点作平行四边形,最多能作( )| A、3个 | B、2个 | C、1个 | D、0个 |
 如图,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,DE∥AB.
如图,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,DE∥AB. 如图,在△ABC中,按要求完成下列各题.
如图,在△ABC中,按要求完成下列各题.