题目内容
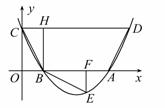
如图,抛物线
 与
与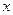 轴交于
轴交于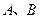 两点,与
两点,与 轴交于
轴交于 点.
点.
(1)请求出抛物线顶点
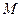 的坐标(用含
的坐标(用含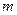 的代数式表示),
的代数式表示),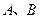 两点的坐标;
两点的坐标;(2)经探究可知,
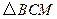 与
与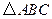 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;(3)是否存在使
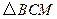 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
(1)
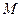 的坐标为(1,
的坐标为(1, m) 两点的坐标为(
m) 两点的坐标为( )、(
)、( )
)(2)

(3)不存在解析:
解:(1)


 抛物线顶点
抛物线顶点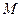 的坐标为(1,
的坐标为(1, m)··················· 2分
m)··················· 2分 抛物线
抛物线 与
与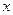 轴交于
轴交于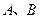 两点,
两点, 当
当 时,
时,

解得

 两点的坐标为(
两点的坐标为( )、(
)、( ). ················· 4分
). ················· 4分(2)当
 时,
时, ,
, 点
点 的坐标为
的坐标为 .
. ················ 5分
················ 5分过点
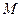 作
作 轴于点
轴于点 ,则
,则


=

=

="3m." ····························· 7分
 ························· 8分
························· 8分(3)存在使
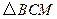 为直角三角形的抛物线.
为直角三角形的抛物线.过点
 作
作 于点
于点 ,则
,则 为
为 ,
,


在
 中,
中,
在
 中,
中,
①如果
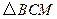 是
是 ,且
,且 那么
那么
即

解得
 ,
,
 存在抛物线
存在抛物线 使得
使得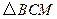 是
是 ;········ 10分
;········ 10分②如果
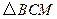 是
是 ,且
,且 那么
那么
即

解得
 ,
,
 存在抛物线
存在抛物线 ,使得
,使得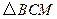 是
是 ;
;③如果
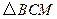 是
是 ,且
,且 ,那么
,那么
即

整理得
 此方程无解.
此方程无解. 以
以 为直角的直角三角形不存在.
为直角的直角三角形不存在.综上所述,存在抛物线
 和
和
使得
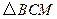 是
是 .························· 12分
.························· 12分 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
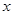 轴交于
轴交于 (2)点
(2)点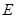 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以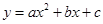 与
与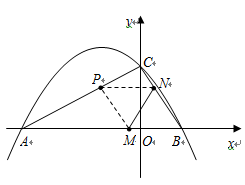
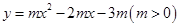 与
与 轴交于
轴交于 两点,与
两点,与 轴交于
轴交于 点.
点.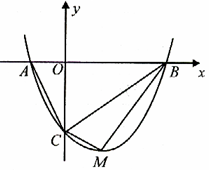
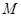 的坐标(用含
的坐标(用含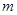 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;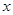 轴交于
轴交于 (
( ,0)、
,0)、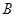 (
( ,0)两点,且
,0)两点,且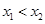 ,与
,与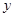 轴交于点
轴交于点 ,其中
,其中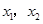 是方程
是方程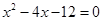 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段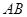 上的一个动点,过点
上的一个动点,过点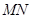 ∥
∥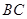 ,交
,交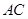 于点
于点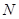 ,连接
,连接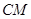 ,当
,当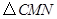 的面积最大时,求点
的面积最大时,求点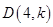 在(1)中抛物线上,
在(1)中抛物线上,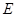 为抛物线上一动点,在
为抛物线上一动点,在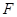 ,使以
,使以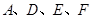 为顶
为顶