题目内容
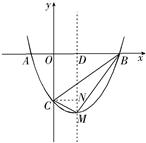
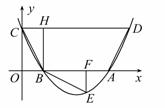
如图,抛物线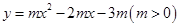 与
与 轴交于
轴交于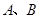 两点,与
两点,与 轴交于
轴交于 点.
点.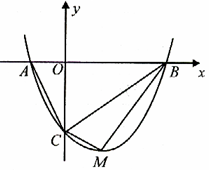
(1)请求出抛物线顶点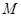 的坐标(用含
的坐标(用含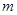 的代数式表示),
的代数式表示),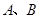 两点的坐标;
两点的坐标;
(2)经探究可知, 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;
(3)是否存在使 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
解析试题分析:(1)将抛物线的解析式化为顶点坐标式,即可得到顶点M的坐标;抛物线的解析式中,令y=0,可求得A、B的坐标.
(2)易求得C点坐标,即可得到OC的长,以AB为底,OC为高,即可求出△ABC的面积;△BCM的面积无法直接求得,可用割补法求解,过M作MD⊥x轴于D,根据B、C、M四点坐标,可分别求出梯形OCMD、△BDM的面积,它们的面积和减去△BOC的面积即为△BCM的面积,进而可得到△ABC、△BCM的面积比.
(3)首先根据B、C、M的坐标,求出BC2、BM2、CM2的值,由于△BCM中,B、C、M都有可能是直角顶点,所以要分三种情况讨论:①∠BCM=90°,②∠BMC=90°,③∠MBC=90°,在上述三种不同的直角三角形中,利用勾股定理可求得m的值,进而可确定抛物线的解析式.
(1)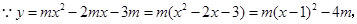
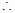 抛物线顶点
抛物线顶点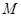 的坐标为(1,
的坐标为(1, m)
m)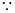 抛物线
抛物线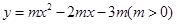 与
与 轴交于
轴交于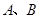 两点,
两点, 当
当 时,
时,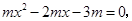
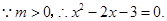
解得
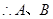 两点的坐标为(
两点的坐标为( )、(
)、(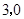 );
);
(2)当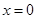 时,
时, ,
,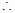 点
点 的坐标为
的坐标为 .
.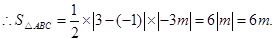 5分
5分
过点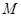 作
作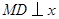 轴于点
轴于点 ,则
,则
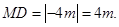
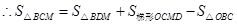
=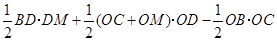
=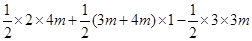
=3m
(3)存在使 为直角三角形的抛物线.
为直角三角形的抛物线.
过点 作
作 于点
于点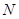 ,则
,则 为
为 ,
,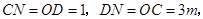
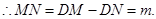
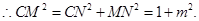
在 中,
中,
在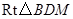 中,
中,
①如果 是
是 ,且
,且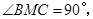 那么
那么
即
解得 ,
,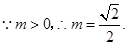
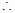 存在抛物线
存在抛物线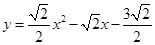 使得
使得 是
是 ;
;
②如果 是
是 ,且
,且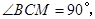 那么
那么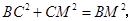
即
解得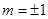 ,
,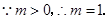
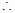 存在抛物线
存在抛物线 ,使得
,使得 是
是 ;
;
③如果 是
是 ,且
,且 ,那么
,那么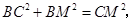
即
整理得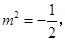 此方程无解.
此方程无解.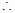 以
以

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
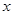 轴交于
轴交于 (2)点
(2)点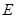 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以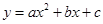 与
与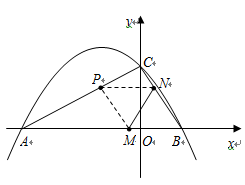
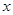 轴交于
轴交于 (
( ,0)、
,0)、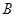 (
( ,0)两点,且
,0)两点,且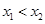 ,与
,与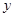 轴交于点
轴交于点 ,其中
,其中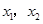 是方程
是方程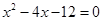 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段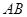 上的一个动点,过点
上的一个动点,过点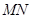 ∥
∥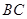 ,交
,交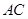 于点
于点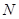 ,连接
,连接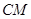 ,当
,当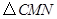 的面积最大时,求点
的面积最大时,求点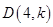 在(1)中抛物线上,
在(1)中抛物线上,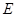 为抛物线上一动点,在
为抛物线上一动点,在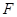 ,使以
,使以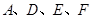 为顶
为顶