题目内容
12. 在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,tan∠MBO=$\frac{2}{3}$,求EM:MF的值.
分析 (1)根据两直线平行,内错角相等可得∠AEO=∠CFO,然后利用“角角边”证明△AEO和△CFO全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相平分的四边形是平行四边形证明即可;
(2)设OM=x,根据∠MBO的正切值表示出BM,再根据△AOM和△OBM相似,利用相似三角形对应边成比例求出AM,然后根据△AEM和△BFM相似,利用相似三角形对应边成比例求解即可.
解答 (1)证明:在菱形ABCD中,AD∥BC,OA=OC,OB=OD,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$,
∴△AEO≌△CFO(AAS),
∴OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形;
(2)解:设OM=2x,
∵EF⊥AB,tan∠MBO=$\frac{2}{3}$,
∴BM=3x,
又∵AC⊥BD,
∴∠AOM=∠OBM,
∴△AOM∽△OBM,
∴$\frac{AM}{OM}$=$\frac{OM}{BM}$,
∴AM=$\frac{O{M}^{2}}{BM}$=$\frac{4}{3}$x,
∵AD∥BC,
∴△AEM∽△BFM,
∴EM:FM=AM:BM=$\frac{4}{3}$x:3x=4:9.
点评 本题考查了菱形的性质,全等三角形的判定与性质,相似三角形的判定与性质,锐角三角函数的定义,难点在于(2)两次求出三角形相似.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.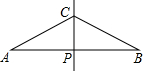 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
 如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:
如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;
乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.
下列说法正确的是( )
| A. | 甲、乙都正确 | B. | 甲、乙都错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
20.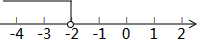 如图,关于x的一元一次不等式ax-2>0的解集在数轴上表示如图,则关于y的方程ay+2=0的解为( )
如图,关于x的一元一次不等式ax-2>0的解集在数轴上表示如图,则关于y的方程ay+2=0的解为( )
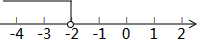 如图,关于x的一元一次不等式ax-2>0的解集在数轴上表示如图,则关于y的方程ay+2=0的解为( )
如图,关于x的一元一次不等式ax-2>0的解集在数轴上表示如图,则关于y的方程ay+2=0的解为( )| A. | y=-2 | B. | y=2 | C. | y=-1 | D. | y=1 |
7.若x=5是关于x的方程2x+3m-1=0的解,则m的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
 如图,在矩形ABCD中,E、F分别在AB、CD上,且DE=BF.求证:四边形DEBF是平行四边形.
如图,在矩形ABCD中,E、F分别在AB、CD上,且DE=BF.求证:四边形DEBF是平行四边形. 如图,若在象棋棋盘上建立直角坐标系,使“帅”位于点(-3,-2),“炮”位于点(-2,0),则“兵”位于的点的坐标为(-5,1).
如图,若在象棋棋盘上建立直角坐标系,使“帅”位于点(-3,-2),“炮”位于点(-2,0),则“兵”位于的点的坐标为(-5,1).