题目内容
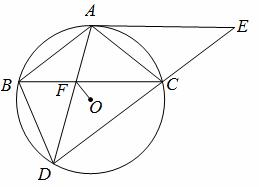
如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
解:(1)证明:如答图1,连接AO并延长交⊙O于另一点G,连接CG,
∵AE是⊙O的切线,∴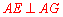 .
.
∴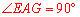 ,即
,即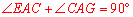 .
.
∵AO是⊙O的直径,∴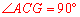 .
.
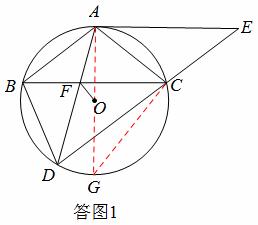
∴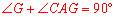 .
.
∴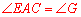 .
.
∵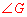 和
和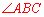 是同圆中同弧所对的圆周角,
是同圆中同弧所对的圆周角,
∴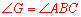 .
.
∴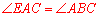 .
.
(学习过弦切角定理的直接得此)
∵AB=AC,∴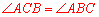 .∴
.∴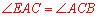 .∴AE∥BC.
.∴AE∥BC.
又∵AB∥CD,∴四边形ABCE是平行四边形.
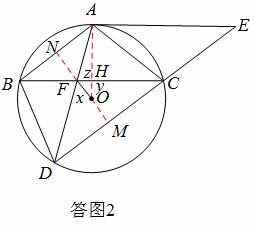
(2)如答图2,连接AO,交BC于点H,双向延长OF分别交AB、CD于点N、M,
∵AE是⊙O的切线,
∴根据切割线定理,得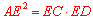 ,(没学习切割线定理可由相似得到)
,(没学习切割线定理可由相似得到)
∵ AE=6,CD=5,∴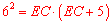 ,解得
,解得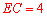 (已舍去负数).
(已舍去负数).
由圆的对称性,知四边形ABDC是等腰梯形,且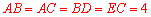 .
.
又根据对称性和垂径定理,知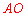 垂直平分
垂直平分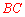 ,
,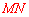 垂直平分
垂直平分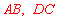 .
.
设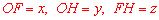 ,
,
∵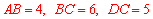
∴ .
.
易证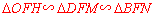 ,
,
∴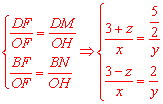 .
.
两式相加和相除,得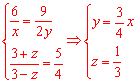 .
.
又∵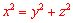 ,∴
,∴ .
.
∴OF的长为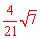 .
.
‘
【考点】切线的性质;圆周勾股定理;等腰三角形的性质;平行的判定;平行四边形的判定和性质;等腰梯形的判定和性质;垂径定理;相似判定和性质;勾股定理.
【分析】(1)作辅助线,连接AO并延长交⊙O于另一点G,连接CG,根据切线的性质证明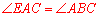 ,根据等腰三角形等边对等角的性质和等量代换得到
,根据等腰三角形等边对等角的性质和等量代换得到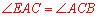 ,从而根据内错角相等两直线平行的判定得到AE∥BC,结合已知AB∥CD即可判定四边形ABCE是平行四边形.
,从而根据内错角相等两直线平行的判定得到AE∥BC,结合已知AB∥CD即可判定四边形ABCE是平行四边形.
(2)作辅助线,连接AO,交BC于点H,双向延长OF分别交AB、CD于点N、M,根据切割线定理求得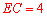 ,证明四边形ABDC是等腰梯形,根据对称性、圆周角定理和垂径定理的综合应用证明
,证明四边形ABDC是等腰梯形,根据对称性、圆周角定理和垂径定理的综合应用证明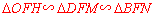 ,并由勾股定理列式求角即可.
,并由勾股定理列式求角即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的倒数是( ) A、-2 B、2 C、
的倒数是( ) A、-2 B、2 C、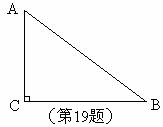
 ,B
,B ,动点C在
,动点C在 轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为【 】
轴上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数为【 】
 B.2 C.3 D.
B.2 C.3 D.
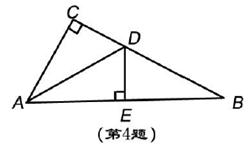
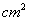 )与高
)与高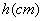 之间的函数关系是为_________________________
之间的函数关系是为_________________________