题目内容
乘法公式的探究及应用．
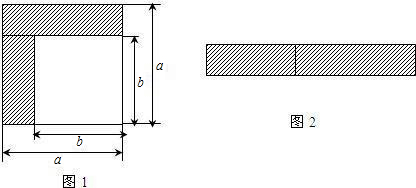
（1）如左图，可以求出阴影部分的面积是 _________ （写成两数平方差的形式）；
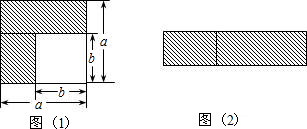
（2）如右图，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是 _________ ，长是 _________ ，面积是 _________ ．（写成多项式乘法的形式）
（3）比较左、右两图的阴影部分面积，可以得到乘法公式 _________ ．（用式子表达）
（4）运用你所得到的公式，计算下列各题：①10.3×9.7；②（2m+n﹣p）（2m﹣n+p）．
（1）如左图，可以求出阴影部分的面积是 _________ （写成两数平方差的形式）；
（2）如右图，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是 _________ ，长是 _________ ，面积是 _________ ．（写成多项式乘法的形式）
（3）比较左、右两图的阴影部分面积，可以得到乘法公式 _________ ．（用式子表达）
（4）运用你所得到的公式，计算下列各题：①10.3×9.7；②（2m+n﹣p）（2m﹣n+p）．
解：（1）利用大正方形面积减去小正方形面积即可求出：a2﹣b2；
（2）它的宽是a﹣b，长是a+b，面积是（a+b）（a﹣b）；
（3）根据题意得出：（a+b）（a﹣b）=a2﹣b2；
（4）①10.3×9.7
=（10+0.3）（10﹣0.3）
=100﹣0.09
=99.91；
②（2m+n﹣p）（2m﹣n+p）
=[2m+（n﹣p）][2m﹣（n﹣p）]
=4m2﹣（n﹣p）2
=4m2﹣n2﹣p2+2np．
（2）它的宽是a﹣b，长是a+b，面积是（a+b）（a﹣b）；
（3）根据题意得出：（a+b）（a﹣b）=a2﹣b2；
（4）①10.3×9.7
=（10+0.3）（10﹣0.3）
=100﹣0.09
=99.91；
②（2m+n﹣p）（2m﹣n+p）
=[2m+（n﹣p）][2m﹣（n﹣p）]
=4m2﹣（n﹣p）2
=4m2﹣n2﹣p2+2np．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
