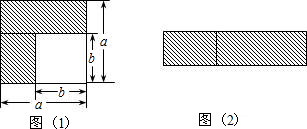
题目内容
乘法公式的探究及应用:(1)如图1所示,可以求出阴影部分的面积是
(2)若将图1中的阴影部分裁剪下来,重新拼成一个如图2的矩形,此矩形的面积是
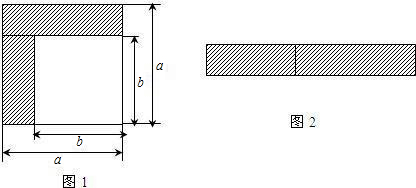
(3)比较两图的阴影部分面积,可以得到乘法公式
(4)应用所得的公式计算:
(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 992 |
| 1 |
| 1002 |
分析:(1)利用面积公式:大正方形的面积-小正方形的面积=阴影面积;
(2)利用矩形公式即可求解;
(3)利用面积相等列出等式即可;
(4)利用平方差公式简便计算.
(2)利用矩形公式即可求解;
(3)利用面积相等列出等式即可;
(4)利用平方差公式简便计算.
解答:解:(1)a2-b2;
(2)(a+b)(a-b);
(3)a2-b2=(a+b)(a-b);
(4)原式=(1-
)(1+
)(1-
)(1+
)…(1-
)(1+
)(1-
)(1+
),
=
×
×
×
×…×
×
×
×
,
=
.
(2)(a+b)(a-b);
(3)a2-b2=(a+b)(a-b);
(4)原式=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 100 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 98 |
| 99 |
| 100 |
| 99 |
| 99 |
| 100 |
| 101 |
| 100 |
=
| 101 |
| 200 |
点评:本题综合考查了证明平方差公式和使用平方差公式的能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目