Question

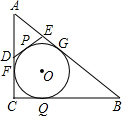如图，Rt△ABC中，∠C=90°，∠A=45°，点P是它的内切圆⊙O两切点F，G之间劣弧上任一点，过P作⊙O的切线交AC，AB于D，E，当⊙O的半径为1时，△ADE的周长为

1. A.
   4
2. B.
   2
3. C.
   2+
4. D.
   2+2

Answer 1

D
分析：连接OF，OQ，四边形OFCQ为正方形，设AF=x，则BQ=BG=AG=x，根据勾股定理列出关于x的一元二次方程2（x+1）²=4x²，△ADE的周长就等于AF+AG．
解答：解：连接OF，OQ，∴OF=OQ，∴四边形OFCQ为正方形，
设AF=x，则BQ=BG=AG=x，
∴根据勾股定理得2（x+1）²=4x²，
解得x=1±（舍去负号），
∵DE是⊙O的切线，∴DF=DP，EP=EG，
∴△ADE的周长=AF+AG=2x=2（1+），
故选D．
点评：本题考查了切线长定理、等腰三角形的性质和三角形的内切圆．