Question

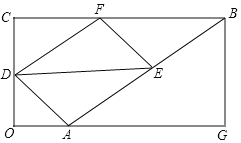
【题目】已知：如图，在中，分别是、的中点，分别是对角线上的四等分点，顺次连接.

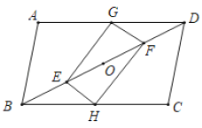
（1）求证：四边形是平行四边形；

（2）当满足____ 条件时，四边形是菱形；

（3）若，

①探究四边形的形状，并说明理由；

②当时，直接写出四边形的面积.

Answer 1

【答案】(1)见解析;(2) 当满足条件时，四边形是菱形，理由见解析；（3）①四边形是矩形，理由见解析；②

【解析】

（1）连接AC，由平行四边形的性质和已知条件得出E、F分别为OB、OD的中点，证出GF为△AOD的中位线，由三角形中位线定理得出GF∥OA，OA，同理：EH∥OC，，得出EH=GF，EH∥GF，即可得出结论；

（2）连接GH，证出四边形ABHG是平行四边形，再证明GH⊥EF，即可得出四边形GEHF是菱形；

（3）①由（2）得：四边形GEHF是平行四边形，得出GH=AB，证出GH=EF，即可得出四边形GEHF是矩形；

②作AM⊥BD于M，GN⊥BD于N，则AM∥GN，证出GN是△ADM的中位线，得出，证出∠BAM=30°，由直角三角形的性质得出，，得出，求出△EFG的面积=，即可得出结果．

（1）证明：连接，如图所示：

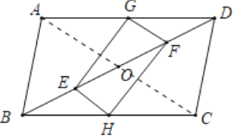
∵四边形是平行四边形，

∴，

∴的中点在上，

∵分别是对角线上的四等分点，

∴分别为、的中点，

∵是的中点，

∴为的中位线，

∴GF∥OA，OA，

同理：EH∥OC，

∴EH=GF，EH∥GF，

∴四边形是平行四边形；

（2）解：当满足条件时，四边形是菱形；理由如下：

连接，如图所示：

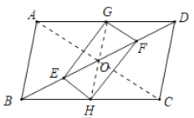
则AG=BH，AG∥BH，

∴四边形是平行四边形，

∴AB∥GH，

∵，

∴，

∴，

∴四边形是菱形；

故答案为：；

（3）解：①四边形是矩形；理由如下：

由（2）得：四边形是平行四边形，

∴，

∵，

∴，

∴，

∴四边形是矩形；

②作于，于，如图所示：

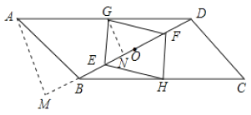
则AM∥GN，

∵是的中点，

∴是的中位线，

∴，

∵，

∴，

∴，

∴，

∴，

∵，

∴，

∴的面积，

∴四边形的面积的面积.