题目内容
10. 如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.
如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.(Ⅰ)当圆心O移动的距离为1cm时,则⊙O与直线PA的位置关系是相切.
(Ⅱ)若圆心O的移动距离是d,当⊙O与直线PA相交时,则d的取值范围是1cm<d<5cm.
分析 (1)根据点O的位置和移动的距离求得OP的长,然后根据∠P的度数求得点O到PA的距离,从而利用半径与距离的大小关系作出位置关系的判断;
(2)当点O继续向左移动时直线与圆相交,在BP的延长线上有相同的点O″,从而确定d的取值范围.
解答 解:(1)如图,当点O向左移动1cm时,PO′=PO-O′O=3-1=2cm,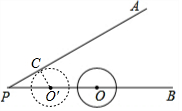
作O′C⊥PA于C,
∵∠P=30度,
∴O′C=$\frac{1}{2}$PO′=1cm,
∵圆的半径为1cm,
∴⊙O与直线PA的位置关系是相切;
(2)如图:当点O由O′向右继续移动时,PA与圆相交,
当移动到C″时,相切,
此时C″P=PO′=2,
∴点O移动的距离d的范围满足1cm<d<5cm时相交,
故答案为:1cm<d<5cm.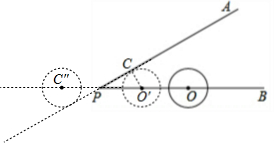
点评 本题考查了直线与圆的位置关系,解题的关键是能够分情况讨论,难度不大.

练习册系列答案
相关题目
5.下列条件是随机事件的是( )
| A. | 通常加热到100℃时,水沸腾 | |
| B. | 在只装有黑球和白球的袋子里,摸出红球 | |
| C. | 购买一张彩票,中奖 | |
| D. | 太阳从东方升起 |
15.下列运算正确的是( )
| A. | a2+a4=2a2 | B. | 3a2-2a2=1 | C. | 3a-a=3 | D. | 3a2-4a2=-a2 |
2.某市2016年10月份某日的一天的温差为9℃,最高温度为t℃,则最低气温可表示为( )
| A. | (t-9)℃ | B. | (9-t)℃ | C. | (-9-t)℃ | D. | (t+9)℃ |
19.松北某超市今年一月份的营业额为50万元.三月份的营业额为72万元.则二、三两个月平均每月营业额的增长率是( )
| A. | 25% | B. | 20% | C. | 15% | D. | 10% |
 分别在如图的圆圈内填入不同的整数,使得每条线上的3个数之和都为0,至少写出三种答案.
分别在如图的圆圈内填入不同的整数,使得每条线上的3个数之和都为0,至少写出三种答案. 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处.分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.