题目内容
 如图,直线y=kx+b与坐标轴的两个交点分别为A(2,0)和B(0,-3),则不等式kx+b+3≥0的解集是
如图,直线y=kx+b与坐标轴的两个交点分别为A(2,0)和B(0,-3),则不等式kx+b+3≥0的解集是
- A.x≥0
- B.x≤0
- C.x≥2
- D.x≤2
A
分析:从图象上知,直线y=kx+b的函数值y随x的增大而增大,与y轴的交点为B(0,-3),即当x=0时,y=-3,所以当x≥0时,函数值kx+b≥-3.
解答:直线y=kx+b与y轴的交点为B(0,-3),
即当x=0时,y=-3,
由于函数值y随x的增大而增大,
∴当x≥0时,函数值kx+b≥-3,
∴不等式kx+b+3≥0的解集是x≥0.
故选A.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.
分析:从图象上知,直线y=kx+b的函数值y随x的增大而增大,与y轴的交点为B(0,-3),即当x=0时,y=-3,所以当x≥0时,函数值kx+b≥-3.
解答:直线y=kx+b与y轴的交点为B(0,-3),
即当x=0时,y=-3,
由于函数值y随x的增大而增大,
∴当x≥0时,函数值kx+b≥-3,
∴不等式kx+b+3≥0的解集是x≥0.
故选A.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
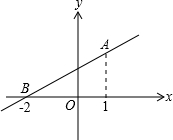 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为