题目内容
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△BED的周长是__________.

8cm.
【考点】角平分线的性质;等腰直角三角形.
【分析】根据角平分线上的点到角的两边的距离相等可得CD=DE,再根据“HL”证明△ACD和△AED全等,根据全等三角形对应边相等可得AC=AE,然后求出△BED的周长=AB,即可得解.
【解答】解:∵∠C=90°,AD平分∠CAB,DE⊥AB,
∴CD=DE,
在△ACD和△AED中,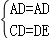 ,
,
∴△ACD≌△AED(HL),
∴AC=AE,
∴△BED的周长=DE+BD+BE,
=BD+CD+BE,
=BC+BE,
=AC+BE,
=AE+BE,
=AB,
∵AB=8cm,
∴△BED的周长是8cm.
故答案为:8cm.
【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,全等三角形的判定与性质,熟记性质并求出△BED的周长=AB是解题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目

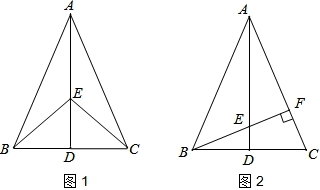



 =
=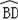
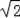
 ,求阴影部分的面积;
,求阴影部分的面积;

 的值为 。
的值为 。